 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Япония >> 1994 | Убрать решения |
|
|
| Японская математическая олимпиада.. 1994 |
|
|
Из множества натуральных чисел выкинули все числа имеющие
вид 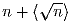 (
(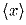 –
ближайшее к x целое число).
an – оставшиеся числа выписали в порядке возрастания.
Найдите формулу для an.
–
ближайшее к x целое число).
an – оставшиеся числа выписали в порядке возрастания.
Найдите формулу для an.
Задача 2:
На плоскости отметили 5 точек никакие три из которых не лежат на одной прямой. Известно, что квадраты 9 из 10 попарных расстояний между этими точками – рациональные числа. Докажите, что и квадрат оставшегося расстояния также рациональное число.
Задача 3:
На плоскости дан треугольник A0A1A2 и точка P0. Строится последовательность точек P1,P2, … Точка Pi + 1 симметрична Pi относительно вершины Ai 3. a) Докажите, что P6 = P0. b) Найдите ГМТ P0 для которых отрезки PiPi + 1 не пересекают внутренность треугольника A0A1A2.
Задача 4:
M – середина сторны BC треугольника ABC. ∠ MAC = 15. Найдите максимально возможное значение угла ∠ B.
Задача 5:
Каждому из N человек дважды выдают карточки на которых написаны числа от 1 до N. Затем некоторым из них выдают подарки в соответствии со следующим правилом: человек получает подарок, если никто другой за обе раздачи карточек не получил числа больше него. Определите ожидаемое количество выданных подарков.
| Задачная база >> Национальные зарубежные олимпиады >> Япония >> 1994 | Убрать решения |