Задача 1:

Числа x и y удовлетворяют следующим соотношениям:  cos x =  cos y,  sin x =  –  sin y. Докажите, что  sin 1994x +  sin 1994y = 0

Задача 2:

???

Задача 3:

Положительные числа a, b, c удовлетворяют равенству a + b + c = abc. Докажите, что по крайней мере одно из чисел a,b,c больше .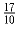

Задача 4:

Решите уравнение в натуральных числах: 1! + 2! + 3! +  …  + n! = m³.

Решение:

Куб натурального числа сравним с  – 1, 0 или 1 по модулю 7. Обозначим S_k = 1! + 2! +  …  + k!, тогда S_k ≡ S_l (mod 7) при k,l ≥ 6. Рассмотрим остатки S_k при делении на 7:

Поскольку S₅ = 153 не является точным кубом, имеем единственное решение n = m = 1.

Задача 5:

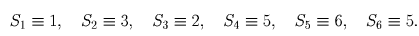
В группе из 1994 человек у каждого 1600 знакомых. Докажите, что можно выбрать 6 человек так, что любые двое из них будут знакомы.