 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Литва >> 1995 | Убрать решения |
|
|
| Литовская математическая олимпиада.. 1995 |
|
|
Дано 10 натуральных чисел. Из 10 всевозможных сумм по 9 всего 9 различных: 86, 87, 88, 89, 90, 91, 93, 94, 95. Найдите исходные числа.
Решение:
Пусть S – сумма всех этих чисел. Тогда, записанные суммы чисел по 9 – S – a1, S – a2,…,S – a10. Будем считать, что первые девять из них различны, тогда их сумма равна 813. Заметим, что сумма всех сумм по 9 равна 9S, то есть делится на 9, следовательно, повторяющаяся сумма – 87 и сумма всех чисел – 100, тогда искомые числа: 5, 6, 7, 9, 10, 11, 12, 13, 13 и 14.
Задача 2:Найдите наименьшее количество натуральных чисел сумма квадратов которых равна 1995.
Задача 3:
В арифметическом треугольнике с основанием 9 расставьте числа от 1 до 9 так, чтобы начиная со второй строчки каждое число было бы равно разности двух чисел стоящих над ним. Всегда ли возможно так расставить числа от 1 до n в треугольнике с основанием n?
Задача 4:
Найдите все функции 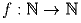 такие, что f(f(m) + f(n)) = m + n для
всех натуральных m и n.
такие, что f(f(m) + f(n)) = m + n для
всех натуральных m и n.
Задача 5:
В трапеции ABCD с основаниями AB = a и CD = b диагонали пересекаются в точке O. Найдите отношение площадей треугольника ABO и трапеции.
Задача 6:
Рассмотрим пары вещественных чисел (x,y), удовлетворяющие неравенствам
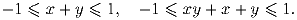
Задача 7:
Число n называется честолюбивым, если после приписывания его к любому натуральному числу справа получается число, делящееся на n. a) Найдите первые 10 честолюбивых чисел. b) Найдите все честолюбивые числа.
Задача 8:
Сумма длин диагоналей трапеции площади 2 равна 4. Докажите, что диагонали перпендикулярны.
Задача 9:
По кругу выписано 100 чисел с суммой 100. Сумма любых 6 идущих подряд чисел не превосходит 6. Одно из записанных чисел – 6. Найдите остальные числа.
Задача 10:
Докажите, что в любой момент времени перемещая часовую и минутную стрелки в положения сииметричные относительно вертикальной прямой (соединяющей отметки 6 и 12) получается положение стрелок правильно показывающее какое-то время. Найдите все прямые, проходящие через центр циферблата обладающие таким свойством.
| Задачная база >> Национальные зарубежные олимпиады >> Литва >> 1995 | Убрать решения |