 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1990 | Убрать решения |
|
|
| Испанская математическая олимпиада.. 1990 |
|
|
x и y – два положительных числа. Покажите, что выражение
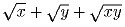 может быть записано в виде
может быть записано в виде
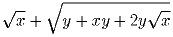
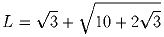
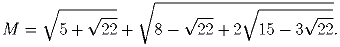
Каждая точка плоскости покрашена в один из трех цветов. Верно ли, что тогда обязательно существуют две точки одного цвета на расстоянии 1 сантиметр?
Задача 3:
Целой частью числа a назовем максимальное целое число не
превосходящее a. Докажите, что целая часть числа 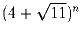 , где
n некоторое целое число, всегда нечетное число.
, где
n некоторое целое число, всегда нечетное число.
Задача 4:
Докажите, что сумма
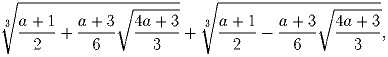
На сторонах BC, CA и AB треугольника ABC, площадь которого
равна S, взяли три точки A′, B′ и C′, таким образом, что
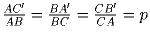 ,
где 0 < p < 1. Найдите:
,
где 0 < p < 1. Найдите:
1) площадь треугольника A′B′C′ как функцию от p;
2) значение p, при котором эта площадь минимальна;
3) геометрическое место точек пересечения прямых A′X и C′Y, проведенных параллельно AB и AC соответственно, при различных p из интервала (0,\,1).
Задача 6:На плоскости дано n точек все попарные расстояния между которыми различны. Каждую точку соединили отрезком с ближайшей к ней. Докажите, что ни одна из точек не соединена с более чем 5 другими.
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1990 | Убрать решения |