 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1995 | Убрать решения |
|
|
| Испанская математическая олимпиада.. 1995 |
|
|
Рассмотрим множество A, состоящее из 100 натуральных чисел, такое, что для любых трех a, b, c из A (не обязательно различных) треугольник, длины сторон которого равны a, b и c не являетс тупоугольным. S(A) – сумма периметров всех таких треугольников со сторонами из A. Найдите минимальное значение S(A).
Задача 2:
Вырежем из бумаги несколько кругов (возможно разного радиуса) и положим их на стол так, что некоторые из них будут налагаться друг на друга, но никакой из кругов не будет полностью содержаться в другом. Затем от каждого круга отрежем ту часть, которая не пересекается с другими кругами. Докажите, что из всех отрезанных кусков нельзя сложить несколько кругов так, чтобы ни одного куска не осталось.
Задача 3:
Через точку G – центр тяжести треугольника ABC, проведем прямую,
которая пересекает стороны AB и AC в точках P и Q соответственно.
Докажите, что
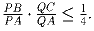
p – простое число. Найдите все целочисленные решения уравнения: p • (x + y) = x • y.
Задача 5:Уравнени x³ + mx – n = 0 и nx² – 2m²x² – 5mnx – 2m³ – n² = 0 (n ≠ 0) имеют общий корень. Докажите, что тогда первое уравнение имеет два равных корня, и найдите корни обеих уравнений как функцию от n.
Задача 6:
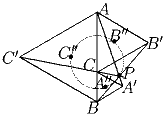
AB – фиксированный отрезок, C – произвольная точка внутри него. Построим два равносторонних треугольника ACB′ и CBA′ в одной полуплоскости относительно прямой AB и равносторонний треугольник ABC′ в другой полуплоскости. Докажите, что:
1) Прямые AA′, BB′ и CC′ пересекаются в одной точке (обозначим эту точку P);
2) Найдите геометрическое место точек P, когда C меняетс внутри отрезка AB;
3) Центры трех треугольников A″,B″,C″ являются вершинами равностороннего треугольника;
4) Точки A″,B″,C″,P лежат на одной окружности.
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1995 | Убрать решения |