 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1997 | Убрать решения |
|
|
| Испанская математическая олимпиада.. 1997 |
|
|
Сосчитайте сумму квадратов первых 100 членов арифметической прогрессии, если известно, что их сумма равна – 1, а сумма членов с четными номерами равна + 1.
Задача 2:Из 9 единичных квадратов сложили большой квадрат 3 × 3. Какое максимальное число точек можно выбрать среди 16 вершин маленьких квадратов, чтобы никакие три точки не были бы вершинами равнобедренного прямоугольного треугольника?

Парабола y = x² + px + q пересекает координатные оси в трех различных точках через которые проведем окружность. Докажите, что существует некоторая точка, общая для всех таких окружностей построенных при различных p и q, и найдите ее.
Задача 4:p – простое число. Найдите все такие целые k, что
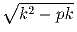 – натуральное число.
– натуральное число.
Задача 5:
Докажите, что сумма длин сторон и диагоналей выпуклого четырехугольника единичной площади не меньше
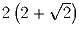 .
.
На кольцевой дороге находится несколько бензоколонок, общее количество бензина в которых хватит на то, чтобы машина объехала полный круг. Первоначально бак машины пуст. Докажите, что вне зависимости от распределения бензина по бензоколонкам выехав из некоторой точки на дороге в некотором направлении можно объехать полный круг по дороге заправляясь на бензоколонках (бак машины считаем достаточно большим, чтобы вместить весь бензин).
| Задачная база >> Национальные зарубежные олимпиады >> Испания >> 1997 | Убрать решения |