 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1993 >> 1 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1993. 1 тур |
|
|
Решите уравнение в вещественных числах:
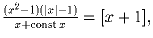 где
где 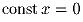 если x = 0, + 1 при x > 0 и – 1 при x < 0.
если x = 0, + 1 при x > 0 и – 1 при x < 0.
n ≥ 3 – натуральное число. Решите систему уравнений
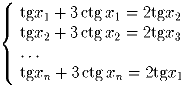
У шестиугольника ABCDEF есть центр симметрии. Прямые AB и EF пересекаются в точке A′, BC и AF – в точке B′, AB и CD – в точке C′. Докажите, что AB • BC • CD = AA′ • BB′ • CC′.
Задача 4:Найдите все функции f определенные на вещественной оси такие, что f(x + y) – f(x – y) = f(x)f(y) для всех вещественных x и y.
Задача 5:
На границе полуплоскости взяли две точки A и C. Для каждой точки полуплоскости B рассмотрим квадраты ABKL и BCMN, построенные внешним образом к треугольнику ABC. Докажите, что все прямые LM при различных точках B имеют общую точку.
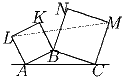
Задача 6:
Дана последовательность xn:
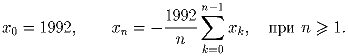
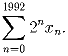
Четыре точки пространства заданы своими координатами:
A0 = (0,0,0); A1 = (1,0,0); A2 = (0,1,0) и A3 = (0,0,1). Точки
Pij определяются из условий
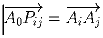 . Найдите объем
наименьшего выпуклого многогранника, содержащего все точки Pij.
. Найдите объем
наименьшего выпуклого многогранника, содержащего все точки Pij.
n ≥ 2 – натуральное число. Определите максимальное значение
суммы натуральных чисел k1,k2, … ,kn, которые удовлетворяют
неравенству
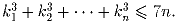
Докажите, что для всех вещественных a,b,c (a² + b² – c²)(b² + c² – a²)(c² + a² – b²) ≤ (a + b – c)²(b + c – a)²(c + a – b)².
Задача 10: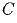 – куб и
– куб и 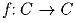 сюръективное
отображение (
сюръективное
отображение (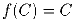 ) такое, что для любых точек
куба P и Q
|PQ| ≥ |f(P)f(Q)|.
) такое, что для любых точек
куба P и Q
|PQ| ≥ |f(P)f(Q)|.
Докажите, что отображение f является изометрией (то есть для любых P и Q из куба |PQ| = |f(P)f(Q)|).
Задача 11:На доску n × n ставят шесть пешек. Пусть pn обозначает
вероятность того, что в каком-то столбце или в какой-то строке стоят 2
пешки. Найдите 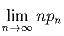 .
.
Докажите, что многочлен xn + 4 разлагается на два множителя с целыми коэффициентами оба из которых имеют степень меньше чем n тогда и только тогда, когда n делится на 4.
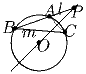
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1993 >> 1 тур | Убрать решения |