 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1993 >> 3 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1993. 3 тур |
|
|
Решите систему уравнений в рациональных числах:
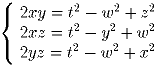
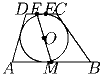
Окружность с центром в точке O, вписанная в неравнобочную трапецию ABCD, касается ее меньшего основания CD в точке E, M – середина AB. Прямая OM пересекает отрезок CD в точке F. Докажите, что |DE| = |FC| тогда и только тогда, когда |AB| = 2|CD|.
Задача 3:
Через g(k) обозначим наибольший нечетный делитель k и положим
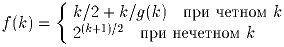
Задача 4:
Вершины выпуклого многогранника, все грани которого треугольники, покрасили в три цвета. Докажите, что число граней все три вершины которых разноцветные – четно.
Задача 5:Найдите все функции заданные на вещественной оси такие, что
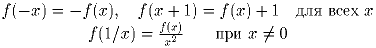
Можно ли найти объем тетраэдра зная площадь его граней и радиус вписанной в него сферы? (иными словами: является ли объем функцией от площадей граней и радиуса вписанной сферы?)
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1993 >> 3 тур | Убрать решения |