 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1994 >> 1 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1994. 1 тур |
|
|
Докажите, что система уравнений
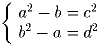
Последовательность функций f1,f2, … задана соотношениями:
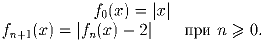
Через точку A внутри окружности с центром O провели хорду PQ отличную от диаметра. Прямые p и q касаются окружности в точках P и Q соответственно, и прямая l, проходящая через точку A перпендикулярно OA, пересекает p и q в точках K и L. Докажите, что |AK| = |AL|.
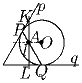
Докажите, что если a, b и c – длины сторон треугольника, то
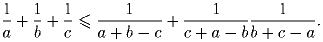
Докажите, что если все три корня многочлена x³ + ax² + bx + c различны, то различными будут и корни многочлена x³ + ax² + ¼(a² + b)x + ⅛(ab – c).
Задача 6:Непрерывная функция f обладает следующим свойством: для любого вещественного x существует такое n, что f f • s f(x) = 1. Докажите, что f(1) = 1.
Задача 7:Дан выпуклый четырехугольник ABCD на сторонах которого внешним образом построены подобные треугольники APB, BQC, CRD и DSA так, что
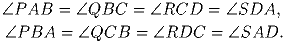
a,b и c – три целых числа таких, что a³ делится на b, b³ делится на c, а c³ делится на a. Докажите, что (a + b + c)¹³ делится на abc.
Задача 9:На конференцию приехало 2n человек каждый из которых знаком не менее чем с n остальными. Докажите, что участников так можно расселить в двухместные номера, чтобы в каждом номере жили знакомые друг с другом люди.
Задача 10:p и q два положительных числа и p + q = 1. Докажите, что для всех натуральных m и n (1 – pm)n + (1 – qn)m ≥ 1.
Задача 11:Пусть r и R – радиусы окружности вписанной в треугольник периметра 2p и окружности описанной вокруг него. Докажите, что p < 2(R + r).
Задача 12:Докажите, что суммы противоположных двугранных углов в тетраэдре равны тогда и только тогда, когда равны суммы длин противоположных сторон.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1994 >> 1 тур | Убрать решения |