 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1995 >> 2 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1995. 2 тур |
|
|
Дан многочлен P(x) с целыми коэффициентами. P(5) делится на 2, P(2) делится на 5. Докажите, что P(7) делится на 10.
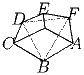
Задача 2:ABCDEF – выпуклый шестиугольник, в котором AB = BC, CD = DE, EF = FA. Докажите, что продолжения высот треугольников BCD, DEF и FAB, опущенных из вершин C, E и A пересекаются в одной точке.
a, b, c, d – положительные иррациональные числа и a + b = 1. Докажите, что c + d = 1 тогда и только тогда, когда для любого натурального n[na] + [nb] = [nc] + [nd].
Задача 4:x1,x2, … ,xn – положительные вещественные числа, удовлетворяющие условию
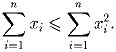
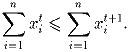
В тетраэдре ABCD, окружности, вписанные в треугольники ABC и ABD, касаются ребра AB в одной точке. Докажите, что точки касания этих окружностей со сторонами AC, BC, AD и BD лежат на одной окружности.
Задача 6:Найдите все натуральные n для которых квадрат n × n можно разрезать на квадраты 2 × 2 и 3 × 3.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1995 >> 2 тур | Убрать решения |