 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1995 >> 3 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1995. 3 тур |
|
|
Сколько существует подмножеств множества 1,2, … ,2n в которых уравнение x + y = 2n + 1 не имеет решений.
Задача 2:Выпуклый пятиугольник разделен диагоналями на один пятиугольник и десять треугольников. Какое максимальное количество равновеликих треугольников могло получиться?
Задача 3:
p – простое число большее 3. Определим последовательность an следующим образом:
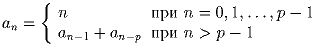
Среднее гармоническое положительных чисел x1,x2, … ,xn равно 1. Найдите минимальное значение
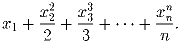
В урне находится n листов бумаги пронумерованных от 1 до n. Из урны один за другим достают листы пока не вытянут лист на котором написано число делящееся на k. При фиксированном n найдите все такие значения k для которых ожидаемое количество вытащенных листов равно k.
Задача 6:Из точки P в пространстве провели три луча k, l и m. A – точка на луче k отличная от P. Докажите, что существует ровно одна пара точек B и C взятых на лучах l и m соответственно, таких, что PA + AB = PC + CB и PB + BC = PA + AC.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1995 >> 3 тур | Убрать решения |