 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1996 >> 3 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1996. 3 тур |
|
|
Найдите все пары (n,r), где n – натуральное число, а r – вещественное, для которых многочлен (x + 1)n – r делится нацело на 2x² + 2x + 1.
Задача 2:Внутри треугольника ABC взяли точку P такую, что ∠ PBC = ∠ PCA < ∠ PAB. Прямая BP пересекает окружность описанную вокруг треугольника ABC в точках B и E. Окружность описанная вокруг треугольника APE пересекается с прямой CE в точках E и F. Докажите, что точки A, P, E и F являются последовательными вершинами четырехугольника и отношение площади четырехугольника APEF к площади треугольника ABP не зависит от выбора точки P.
Задача 3:Дано натуральное число n ≥ 2 и положительные числа a1,a2, … ,an, сумма которых равна 1.
(1) Докажите, что для любых положительных x1,x2, … ,xn, сумма которых равна 1 верно неравенство:
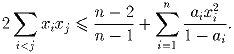
В тетраэдре ABCD ∠ BAC = ∠ ACD и ∠ ABD = ∠ BCD. Докажите, что длины ребер AB и CD равны.
Задача 5:Для натурального k через p(k) обозначим наименьшее простое число не являющееся делителем k. Если p(k) > 2, то определим q(k) как произведение всех простых чисел меньших p(k), а если p(k) = 2, то q(k) = 1. Рассмотрим последовательность xn:
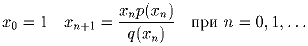
Задача 6:
Из всех перестановок f множества 1,2, … ,n, которые удовлетворяют условию f(i) ≥ i – 1 при i = 1,2, … ,n, выберем наугад одну. Обозначим через pn вероятность того, что выбранная перестановка g удовлетворяет неравенству g(i) ≤ i + 1 при i = 1,2, … ,n. Найдите все n для которых pn > 1/3.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1996 >> 3 тур | Убрать решения |