 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1997 >> 2 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1997. 2 тур |
|
|
Для любого вещественного a найдите число упорядоченных троек вещественных чисел (x,y,z), которые удовлетворяют системе уравнений:
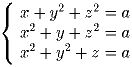
Внутри треугольника ABC выбрали точку P такую, что
∠ PBA = ∠ PCA = ⅓( ∠ ABC + ∠ ACB).
Докажите, что
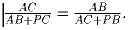
Дано n точек (n ≥ 2) на плоскости никакие три из которых не лежат на одной прямой. Каждые две точки соединили отрезками. Определите наименьшее количество цветов в которые можно покрасить эти отрезки так, чтобы любые два отрезка имеющие выходящие из одной точки были бы покрашены в разные цвета.
Задача 4:Найдите все тройки натуральных чисел обладающие следующим свойством: произведение любых двух чисел дает остаток 1 при делении на третье.
Задача 5:Кидают k белых и m черных костей. Найдите вероятность того, что сумма очков выпавших на белых костях дает такой же остаток при делении на 7 как и сумма очков выпавшая на черных костях.
Задача 6:В кубе со стороной 1 выбрали 8 точек. Докажите, что какие-то две точки являются сторонами отрезка длины не более 1.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1997 >> 2 тур | Убрать решения |