 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1998 >> 2 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1998. 2 тур |
|
|
Пусть An = 1,2, … ,n. Верно ли, что для любого целого n ≥ 2 существуют функции f:An → An и g:An → An такие, что f(f(k)) = g(g(k)) = k для всех k ∈ An; g(f(k)) = k + 1 для всех k < n.
Задача 2:В треугольнике ABC ∠ BCA – тупой и ∠ BAC = 2 ∠ ABC. На прямой AC выбрали точку D такую, что угол DBC прямой, M – середина AB. Докажите, что ∠ AMC = ∠ BMD.
Задача 3:a) a,b,c,d,e,f – неотрицательные числа с суммой 1, удовлетворяюшие неравеству
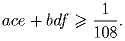
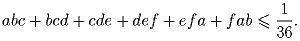
Решите в целых числах уравнение: x² + 3y² = 1998x.
Задача 5:Неотрицательные числа a1,a2, … ,a7,b1,b2, … ,b7 удовлетворяют неравенствам ai + bi ≤ 2 при всех i от 1 до 7. Докажите, что существуют два различных индекса k,m такие, что |ak – am| + |bk – bm| ≤ 1.
Задача 6:Докажите, что в тетраэдре ABCD ребро AB перпендикулярно ребру CD тогда и только тогда, когда существует параллелограм CDPQ такой, что PA = PB = PD и QA = QB = QC.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1998 >> 2 тур | Убрать решения |