 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1999 >> 1 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1999. 1 тур |
|
|
Докажите, что существует бесконечно много составных чисел вида 50n + (50n + 1)50.
Задача 2:
a,b,c,d – вещественные числа. Докажите, что (a + b + c + d)² ≤ 3(a² + b² + c² + d²) + 6ab.
Задача 3:
ABC – равнобедренный прямоугольный треугольник (угол A – прямой). Точка D делит отрезок BC в отнощении 1:2, E – проекция точки B на прямую AD. Найдите угол CED.
Задача 4:
x и y – вещественные числа, притом x + y, x² + y², x³ + y³ и x4 + y4 – целые. Докажите, что при всех n число xn + yn – целое.
Задача 5:
Решите уравнение yx = x50 в натуральных числах.
Задача 6:
P – точка пересечения диагоналей выпуклого четырехугольника ABCD, M – середина стороны AB. Прямая MP пересекает сторону CD в точке Q. Докажите, что отношение площадей треугольников BCP и ADP равно отношению длин отрезков CQ и DQ.
Задача 7:
Найдите все многочлены a0 + a1x + … + anxn, которые имеют ровно n
корней не превосходящих – 1, коэффициенты которых удовлетворяют
равенству 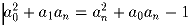 .
.
Задача 8:
Множество S содержит n элементов. Найдите наименьшее количество подмножеств которые можно выбрать из S так, чтобы для любых двух элементов a и b нашлось бы выбранное множество, содержащее ровно один из них.
Задача 9:
На сторонах BC,CA,AB треугольника ABC взяли точки D,E и F соответственно.Окружности, вписанные в треугольники AEF,BFD и CDE касаются окружности, вписанной в треугольник DEF. Докажите, что прямые AD,BE и CF пересекаются в одной точке.
Задача 10:
x1 – положительное вещественное число. Последовательность xn удовлетворяет рекуррентному соотношению
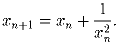
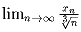 и
найдите его.
и
найдите его.Задача 11:
В урне лежит два шара – черный и белый. Из урны, случайным образом вытаскивают шар, и кладут его обратно, добавляя в урну еще один шар того же цвета. Такую операцию повторили 50 раз. Какое наиболее вероятное количество белых шаров лежит в урне?
Задача 12:
Вершины куба со стороной a лежат на поверхности правильного тетраэдра со стороной 1. Найдите все возможные значения a.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1999 >> 1 тур | Убрать решения |