 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1999 >> 3 тур | Убрать решения |
|
|
| Польская математическая олимпиада.. 1999. 3 тур |
|
|
На стороне BC треугольника ABC взяли точку D такую, что
AD > BC. На стороне AC выбрали точку E, удовлетворяющую
равенству
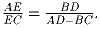 Докажите, что AD > BE.
Докажите, что AD > BE.
Задача 2:
Докажите, что из 101 различного натурального числа меньшего 5050 можно выбрать четыре – a,b,c,d такие, что a + b – c – d делится на 5050.
Решение:Количество возможных пар – 5050, количество возможных в каждой паре разностей – 5048, следовательно найдутся две пары (a,b) и (c,d), разности которых совпадают (a – b = c – d). Но тогда, a + d – b – c = 0, что делится на 5050.
Задача 3:Докажите, что существует 50 различных натуральных чисел n1,n2, … ,n50 таких, что n1 + S(n1) = n2 + S(n2) = … = n50 + S(n50), где S(n) – сумма цифр числа n.
Задача 4:
При каких целых n система уравнений
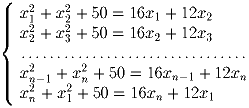
Заметим, что каждое уравнение имеет вид (xi – 8)² + (xi + 1 – 6)² = 50, которое имеет следующие решения в целых числах: xi ∈ 7,9,xi + 1 ∈ – 1,13; xi ∈ 1,15,xi + 1 ∈ 5,7; xi ∈ 3,13,xi + 1 ∈ 1,11. Таким образом пр инекотором i имеем следующую последовательность: xi = 7,xi + 1 = 13,xi + 2 = 1,xi + 3 = 7, … , откуда система имеет решение только при n делящихся на 3.
Задача 5:a1,a2, … ,an,b1, … ,bn – целые числа. Докажите, что
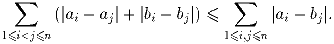
Задача 6:
В выпуклом шестиугольнике ABCDEF сумма углов A, C и E равна 360
и 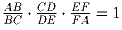 .
Докажите, что
.
Докажите, что 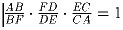 .
.
| Задачная база >> Национальные зарубежные олимпиады >> Польша >> 1999 >> 3 тур | Убрать решения |