 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1997 >> A | Убрать решения |
|
|
| Американская студенческая олимпиада. 1997. A |
|
|
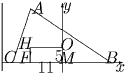
Прямоугольник HOMF имеет стороны HO = 11 и OM = 5. Для треугольника ABC точка H – точка пересечения высот, O – центр описанной окружности, M — середина BC, F – основание высоты, проведенной из вершины A. Найти длину BC.
Решение:По условию сторона BC содержит точки M и F; поэтому точка A лежит на прямой HF. Введем систему координат так, как показано на рисунке.
Точки будут иметь координаты: M(0,0), O(0,5), H( – 11,5), B(x,0), C( – x,0), A( – 11,y). Из условий OA² = OB² и BH ⊥ AC получим соответственно x² + 5² = 11² + (y – 5)² и ( – x – 11)( – x + 11) + 5 • ( – y) = 0. Решая полученную систему, найдем y = 15 и x = 14. Ответ. 28.
Задача 2:
За круглым столом сидят n игроков. Каждый из них первоначально имеет по одному рублю. Первый игрок передает рубль второму, после чего второй передает два рубля третьему. Затем третий игрок передает рубль четвертому, а четвертый два рубля пятому и т.д. Игроки поочередно передают рубль или два рубля следующему игроку, у которого еще есть деньги; игрок, лишившийся денег, выбывает из игры и покидает стол. Найти бесконечное множество таких n, при которых игра заканчивается тем, что у некоторого игрока оказываются все n рублей.
Решение:
После первого круга (т.е. в тот момент, когда n-й игрок уже отдал свои рубли, а следующий по кругу игрок еще не получил) из игры выбывают первый игрок и все игроки с четными номерами, а у оставшихся будет по два рубля. Заметим, что игра сводится к поочередному увеличению или уменьшению количества рублей у игроков на единицу. Поэтому если за столом в течение нескольких кругов игры сидит неизменное четное число игроков, то после каждого круга у одних и тех же игроков количество денег увеличивается, равно как у всех оставшихся уменьшается. В частности, если за столом осталось двое, то через число кругов, равное количеству рублей у того игрока, который каждый раз получая рубль отдает два, игра закончится полной победой его партнера.
Если n = 2k + 1 или n = 2k + 2, то после первого круга за столом останется 2k – 1 игроков, и у каждого будет по 2 рубля. После еще двух кругов число игроков вдвое уменьшится, а у оставшихся будет по 4 рубля. Следующее изменение числа игроков произойдет еще через 4 круга и т.д. Пока игра не кончится, после каждого очередного круга за столом будет сидеть четное число игроков, причем у всех игроков, занимающих четные места, одинаковое число денег, поровну денег будет и у всех игроков, занимающих нечетные места. Поэтому всякое изменение числа игроков (после некоторого круга игры; исключение – первый круг) является уменьшением вдвое. В конце концов за столом останется один победитель с n рублями (общее количество денег во время игры не меняется).
Замечание. Нетрудно показать, что при n, отличном от n = 2k + 1 и n = 2k + 2, игра никогда не кончится.
Задача 3: Вычислить
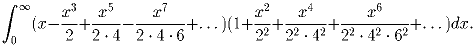
Решение: В первой паре скобок записано разложение в ряд Маклорена функции
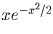 . Почленно интегрируя и учитывая, что
. Почленно интегрируя и учитывая, что
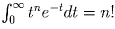 , получим
, получим
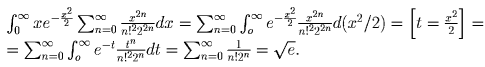
Пусть G – группа с единичным элементом e; φ : G → G – функция такая, что φ (g1) φ (g2) φ (g3) = φ (h1) φ (h2) φ (h3), всякий раз, когда g1g2g3 = e = h1h2h3. Доказать, что существует такой элемент a ∈ G, что функция ψ (x) = a φ (x) есть гомоморфизм (т.е. ψ (xy) = ψ (x) ψ (y) для всех x,y ∈ G).
Решение: Если a φ (x) – гомоморфизм, то a φ (xy) = a φ (x)a φ (y), или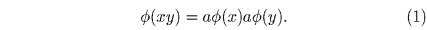
Заметим сначала, что exx – 1 = e = eee, откуда
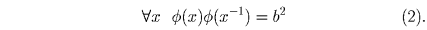
Поскольку x – 1 • xy • y – 1 = e = eee, имеем
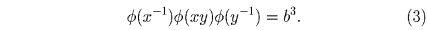
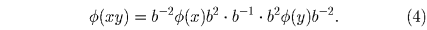
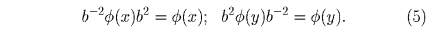
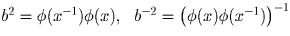 и
и
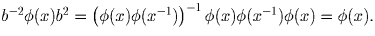 Аналогично доказывается второе соотношение (5).
Итак, из соотношений (4),(5) следует: φ (xy) = φ (x)b – 1 φ (y),
что и требовалось доказать.
Аналогично доказывается второе соотношение (5).
Итак, из соотношений (4),(5) следует: φ (xy) = φ (x)b – 1 φ (y),
что и требовалось доказать.Задача 5:
Для n = 10 определить, четно или нечетно число упорядоченных n-элементных наборов натуральных чисел (x1,x2, … ,xn) таких, что
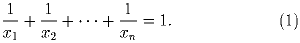
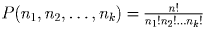 перестановок указанного
набора. На четность общего количества решений влияют только такие наборы,
число перестановок которых нечетно. Нетрудно показать, что число
P(n1,n2, … ,nk) делится на любой биномиальный коэффициент
перестановок указанного
набора. На четность общего количества решений влияют только такие наборы,
число перестановок которых нечетно. Нетрудно показать, что число
P(n1,n2, … ,nk) делится на любой биномиальный коэффициент 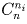 ,
где i = 1, … ,k, n = n1 + … + nk. В условии задачи n = 10. Из чисел
,
где i = 1, … ,k, n = n1 + … + nk. В условии задачи n = 10. Из чисел
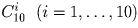 нечетными являются только числа
нечетными являются только числа 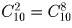 и
и 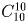 . С учетом того, что число P(2,2,2,2,2)
является четным (это легко проверить), рассмотрению подлежат
лишь следующие варианты.
. С учетом того, что число P(2,2,2,2,2)
является четным (это легко проверить), рассмотрению подлежат
лишь следующие варианты.
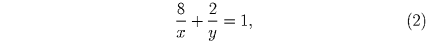
Выразив из уравнения (2) переменную x через переменную y, получим
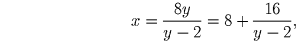
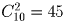 решений уравнения (1).
решений уравнения (1).
Пусть n – натуральное число, c – действительное число. Последовательность (xk) определяется соотношениями x0 = 0,x1 = 1 и
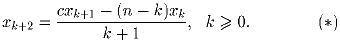
Перепишем соотношение (*) в виде (n – k)xk + (k + 1)xk + 2 = cxk + 1,k = 0,1, … ,n – 1. С учетом условий x0 = xn = 0, x1 = 1 получим матричное уравнение Ax = cx, где A – трехдиагональная матрица, x – вектор-столбец:
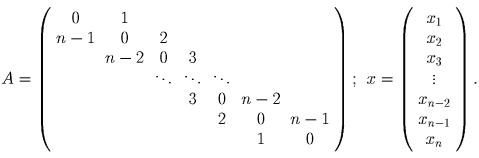
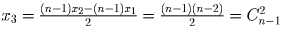 .
Далее индукцией по k легко доказать, что для k = 1,2, … ,n выполняется
равенство
.
Далее индукцией по k легко доказать, что для k = 1,2, … ,n выполняется
равенство 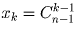 .
.
| Задачная база >> Национальные зарубежные олимпиады >> Putnam >> 1997 >> A | Убрать решения |