 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1989 | Убрать решения |
|
|
| Математическая олимпиада США. 1989 |
|
|
Для натурального n обозначим:
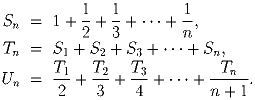
Задача 2:
20 теннисистов устроили между собой соревнование из 14 игр. В каждой игре участвует 2 человека и каждый из этой компании теннисистов принял участие хотя бы в одной игре. Докажите, что в некоторых 6 играх участвовало 12 различных теннисистов.
Задача 3:
P(z) = zn + c1zn – 1 + c2zn – 2 + • s + cn – многочлен с вещественными коэффициентами. Известно, что |P(i)| < 1. Докажите, что существуют такие вещественные числа a и b, что P(a + bi) = 0 и (a² + b² + 1)² < 4b² + 1.
Задача 4:
В остроугольном треугольнике ABC AB < AC < BC, I – центр вписанной окружности, O – центр описанной окружности. Докажите, что прямая IO пересекает стороны AB и BC.
Задача 5:
Какое из двух вещественных чисел u и v больше, если
(u + u² + u³ + • s + u8) + 10u9 = (v + v² + v³ + • s + v¹º) + 10v¹¹ = 8.
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1989 | Убрать решения |