 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1991 | Убрать решения |
|
|
| Математическая олимпиада США. 1991 |
|
|
В треугольнике ABC угол A в два раза больше угла B, угол C – тупой, а длины сторон a,b,c – целые числа. Найдите периметр треугольника, если известно, что он минимальный из всех возможных.
Задача 2:Для любого непустого множества чисел S, обозначим σ (S) и π (S) сумму и произведение элементов S соответственно. Докажите, что
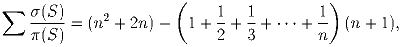
Докажите, что для любого целого n ≥ 1, последовательность
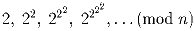
(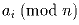 означает взятие остатка от делени
\,ai\, на \,n.)
означает взятие остатка от делени
\,ai\, на \,n.)
Задача 4:
a = (mm + 1 + nn + 1)/(mm + nn), где m и n – натуральные числа. Докажите, что am + an ≥ mm + nn.
Задача 5:D – некоторая точка на стороне AB треугольника ABC, а E – точка, в которой CD пересекает внешнюю общую касательную к окружностям, вписанным в треугольники ACD и BCD. Докажите, что если точка D пробегает отрезок AB, то точка E описывает некоторую дугу окружности.
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1991 | Убрать решения |