 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1992 | Убрать решения |
|
|
| Математическая олимпиада США. 1992 |
|
|
Чему равна сумма цифр числа
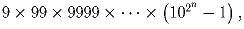 (каждый следующий множитель имеет в два раза больше цифр, чем предыдущий)
(каждый следующий множитель имеет в два раза больше цифр, чем предыдущий)
Задача 2:
Докажите, что
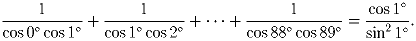
Задача 3:
Обозначим сумму всех элементов непустого множества S через σ (S). Пусть A = a1,a2, … ,a11 – множество натуральных чисел такое, что a1 < a2 < • s < a11 и для каждого натурального n ≤ 1500 существует такое S – подмножество A, дл которого σ (S) = n. Какое наименьшее возможное значение a10?
Задача 4:
Три хорды на сфере (AA′,BB′,CC′) пересекаются в одной точке внутри сферы (P) и не лежат в одной плоскости. Сфера, проходящая через A,B,C,P касается сферы, проходящей через A′,B′,C′,P. Докажите, что AA′ = BB′ = CC′.
Задача 5:P(z) – многочлен 1992 степени с комплексными коэффициентами, все корни которого различны. Докажите, что существуют такие комплексные числа a1,a2, … ,a1992, что P(z) делит многочлен
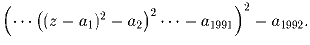
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1992 | Убрать решения |