 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1994 | Убрать решения |
|
|
| Математическая олимпиада США. 1994 |
|
|
k1 < k2 < k3 < • s – последовательность натуральных чисел никакие два из которых не являютс последовательными. sm = k1 + … + km. Докажите, что для любого n в интервале [sn,sn + 1) содержится по крайней мере один точный квадрат.
Задача 2:
Стороны 99-угольника покрашены в три цвета следующим образом: красный, синий, красный, синий, красный, …, красный, синий, желтый. У любой стороны можно поменять цвет на любой другой (синий, красный или желтый) так, чтобы никакие две соседние стороны не были бы окрашены в один и тот же цвет. Можно ли такими перекрашиваниями добиться того, чтобы стороны были бы покрашены вот так: красный, синий, красный, синий, красный, …, красный, желтый, синий?
Задача 3:
ABCDEF – выпуклый шестиугольник, вписанный в окружность, диагонали которого, AD, BE и CF, пересекаются в одной точке и длины сторон AB, CD и EF равны. P – точка пересечения прямых AD и CE. Докажите, что CP/PE = (AC/CE)².
Задача 4:a1,a2,a3, … – последовательность положительных
вещественных чисел такая, что 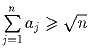 дл
всех натуральных n. Докажите, что
дл
всех натуральных n. Докажите, что
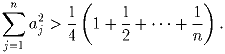
Пусть |U|, σ (U) и π (U) соответственно обозначают количество, сумму и произведение элементов конечного множества натуральных чисел U. (Если U – пустое множество, будем считать, что |U| = 0, σ (U) = 0 и π (U) = 1.) Пусть S – некоторое конечное множество натуральных чисел. Докажите, что дл любого m ≥ σ (S):
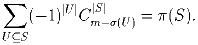
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1994 | Убрать решения |