 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1997 | Убрать решения |
|
|
| Математическая олимпиада США. 1997 |
|
|
p1,p2,p3, … – последовательность всех простых чисел, выписанных в порядке возрастания, x0 – вещественное число между 0 и 1. Для натурального k определим
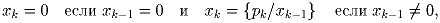
Задача 2:
На сторонах треугольника ABC внешним образом построили равнобедренные треугольники BCD,CAE,ABF, при этом стороны исходного треугольника послужили основаниями для построенных. Докажите что прямые, проходящие через точки A,B,C перпендикулярные прямым EF,FD,DE соответственно, пересекаются в одной точке.
Задача 3:
Докажите, что для любого целого числа n существует единственный многочлен Q с коэффициентами из множества 0,1, … ,9 такой, что Q( – 2) = Q( – 5) = n.
Задача 4:
Урезанием
выпуклого n-угольника назовем выбор
некоторой пары соседних сторон AB и BC, и отрезание треугольника
MBN, где M – середина AB, а N – середина BC, в результате
получается выпуклый (n + 1)-угольник. Правильный шестиугольник 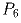 урезали до семиугольника
урезали до семиугольника 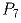 , его, в свою очередь до
восьмиугольника
, его, в свою очередь до
восьмиугольника 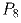 (каким-то из семи возможных способов)б и так
далее. Докажите, что вне зависимости от урезаний площадь
(каким-то из семи возможных способов)б и так
далее. Докажите, что вне зависимости от урезаний площадь 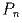 всегда больше 1/3.
всегда больше 1/3.
Докажите, что для любых положительных вещественных a,b,c
(a³ + b³ + abc) – 1 + (b³ + c³ + abc) – 1 + (c³ + a³ + abc) – 1 ≤ (abc) – 1.
Задача 6:a1,a2, … ,a1997 – последовательность неотрицательных целых чисел удовлетворяющая для всех i,j ≥ 1, i + j ≤ 1997 следующему условию:
ai + aj ≤ ai + j ≤ ai + aj + 1. Докажите, что существует вещественное число x такое, что an = [nx] (целая часть числа nx).
| Задачная база >> Национальные зарубежные олимпиады >> США >> 1997 | Убрать решения |