 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Югославия >> Югославская олимпиада. >> 1995 | Убрать решения |
|
|
| Югославская олимпиада.. 1995 |
|
|
Докажите, что если p – простое число, то 11 … 122 … 2 … 99 … 9 – 123456789 делится на p (в записи числа 11 … 9 каждая цифра повторяется p раз).
Решение:
Очевидно, что утверждение верно для p = 2,3,5.
В остальных случаях 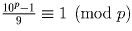 и
10kp ≡ 10k (mod p), тогда
и
10kp ≡ 10k (mod p), тогда
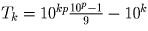 делится на p.
Осталось заметить, что
11 … 122 … 233 … 899 … 9 = 9T0 + 8T1 + 7T2 + … + T8.
делится на p.
Осталось заметить, что
11 … 122 … 233 … 899 … 9 = 9T0 + 8T1 + 7T2 + … + T8.
Значения многочлена P(x) = anxn + an – 1xn – 1 + … + a0 с целыми коэффициентами делятся на m при любом целом x. Докажите, что k!ak делится на m.
Задача 3:
Дана окружность k. M – точка пересечения диаметра CD и перпендикулярной ему хорды AB. На дуге ACB взяли точку P отличную от A, B и C. Прямая PM вторично пересекает окружность k в точке M, R – точка пересечения прямой PD и отрезка AB. Докажите, что RD > MQ.
Задача 4:
В тетраэдре ABCD точки P и Q – середины ребер AB и CD соответственно. Докажите, что если центр сферы описанной около тетраэдра лежит на прямой PQ, то и центр вписанной в него сферы также лежит на этой прямой.
| Задачная база >> Национальные зарубежные олимпиады >> Югославия >> Югославская олимпиада. >> 1995 | Убрать решения |