Задача 1: Найдите все тройки положительных рациональных чисел (x,y,z) с
x ≤ y ≤ z для которых числа xyz, x + y + z и 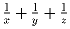 –
целые.
–
целые.
Задача 2: В двоичной записи числа n ровно 1995 единиц. Докажите, что n! делится на
2n – 1995.
Решение: Докажем, что для числа n в двоичной записи которого ровно k единиц
n! делится на 2n – k индукцией по k. База k = 1 очевидна.
Пусть в двоичной записи n – k + 1 единица, тогда n = 2s + n′,
где s ≥ k, а количество единиц в двоичной записи n′ равно k.
Степень, в которой 2 входит в разложение n! на простые множители
равна
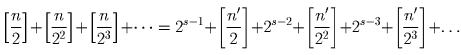
Обозначим
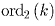
– степень, в которой двойка входит
в разложение числа k на простые множители. Тогда
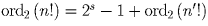
. Поскольку в двоичной записи n′ ровно k
единиц
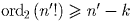
, откуда
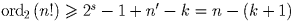
.
Задача 3: В пирамиде SABCD с основанием ABCD все ребра равны между собой.
На ребрах BC и AS выбрали точки M и N соответственно так,
что прямая MN перпендикулярна AD и BC. Найдите BM/MC и SN/NA.


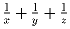 –
целые.
–
целые.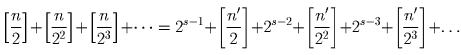
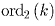 – степень, в которой двойка входит
в разложение числа k на простые множители. Тогда
– степень, в которой двойка входит
в разложение числа k на простые множители. Тогда 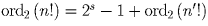 . Поскольку в двоичной записи n′ ровно k
единиц
. Поскольку в двоичной записи n′ ровно k
единиц 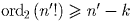 , откуда
, откуда
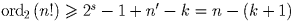 .
Задача 3:
.
Задача 3: