Задача 1:

Задача 2: Доказать, что

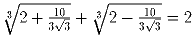
Решение: Воспользовавшись равенством

получим требуемое.

Задача 3:

Задача 4: Точка O – середина высоты правильного тетраэдра ABCD. Через точку O проведены всевозможные прямые, отрезки которых, заключенные внутри ABCD, делятся в точке O пополам. Какое множество образуют концы этих отрезков на поверхности тетраэдра?

Решение: Построим тетраэдр, центральносимметричный данному относительно точки O. Искомое множество является множеством точек пересечения поверхностей исходного и полученного тетраэдров, то есть это шестизвенная ломаная с вершинами на каждой боковой грани и каждом боковом ребре тетраэдра, и еще две точки – концы высоты. Чтобы найти положение вершин ломаной на ребрах и на гранях, рассмотрим сечение тетраэдра, содержащее боковое ребро и высоту. Пусть точки X и Y – вершины ломаной, принадлежащей этому сечению. KD₁ = DM, так как картинка симметрична относительно точки O. KD₁ = ½D₁B, так как D₁ – центр основания тетраэдра. Из подобия треугольников DMX и BD₁X заключаем, что DX:XB = DM:D₁B, то есть DX = ½BX. Из аналогичных соображений KY = ½DY, то есть Y – центр боковой грани тетраэдра. Таким образом окончательный ответ: искомым множеством является шестизвенная ломаная с вершинами в центрах боковых граней и в точках, делящих боковые ребра в отношении 2:1, считая от основания тетраэдра, а также две точки – концы высоты тетраэдра.