Задача 1:
Задача 2:
Задача 3:
Задача 4:
m,n – натуральные числа.
Известно, что
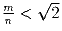
. Доказать,
что
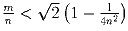
.
Решение:
Из условия
следует, что m² < 2n². Так как m и n – целые числа, то
m² ≤ 2n² – 1. Следовательно,
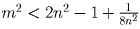
, а последнее неравенство эквивалентно
требуемому.
Задача 5:
Докажите, что уравнение sin ( sin x + x² + 1) + ( sin x + x² + 1)² = x – 1 не имеет вещественных корней.
Решение:
Уравнение имеет вид f(f(x)) = x, где f(x) = x² + 1 + sin x.
Заметим,
что f(x) ≥ x² для любого x. Значит, x = f(f(x)) ≥ (f(x))² ≥ x
4,
откуда
0 ≤ x ≤ 1 и |f(x)| ≤ 1. На промежутке [0,1] f(x)
возрастает, откуда f(x) ≥ f(0) = 1. Но поскольку |f(x)| ≤ 1,
то f(x) = 1, x = 0. Осталось заметить, что x = 0 не является корнем
нашего уравнения.


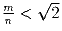 . Доказать,
что
. Доказать,
что 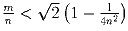 .
.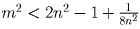 , а последнее неравенство эквивалентно
требуемому.
, а последнее неравенство эквивалентно
требуемому.