Задача 1: Периметр квадрата увеличили на 40, затем периметр полученного квадрата уменьшили на 40. У какого из квадратов площадь наименьшая?

Решение: Чем больше периметр квадрата, тем больше его площадь. 40 от периметра второго квадрата больше, чем 40 от периметра первого. Значит, наименьший периметр, а тогда и наименьшая площадь у третьего квадрата.

Задача 2: Найдите последнюю цифру числа 1² + 2² +  …  + 99².

Решение: Последние цифры сумм

одинаковы. Сумма десяти слагаемых с одной и той же последней цифрой оканчивается нулем.

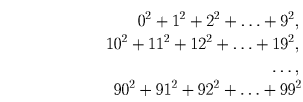
Задача 3: Существует ли число, у которого произведение цифр равно 1980?

Решение: Такого числа не существует, поскольку 1980 = 2 • 2 • 3 • 5 • 11, а произведение цифр не может содержать множителя 11 (так как цифры это: 0,…9).

Задача 4: С набором из пяти чисел, каждое из которых равно 1 или  – 1, разрешено производить следующую операцию: менять знаки у каких-нибудь двух чисел. Можно ли с помощью нескольких таких операций из набора 1, – 1, – 1,1,1 получить набор  – 1,1,1,1,1?

Решение: Нельзя. После такой операции произведение всех написанных на доске чисел не изменяется (или, что то же самое, не изменяется четность количества «минус единиц"), а для начального и конечного наборов эти произведения отличаются.