Задача 1: Число членов арифметической прогрессии нечетно. Сумма членов прогрессии, стоящих на местах с четными номерами, равна сумме членов, стоящих на местах с нечетными номерами. Найдите сумму всех членов прогрессии.

Решение: Члены, стоящие на четных местах, и члены, стоящие на нечетных местах, образуют арифметические прогрессии. Приравняем их суммы: 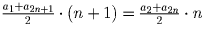. Так как a₁ + a_2n + 1 = a₂ + a_2n, то это равенство возможно только при a₁ + a_2n + 1 = 0. Но тогда и сумма всех членов прогрессии, вычисляемая по формуле 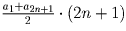, равна нулю.

Задача 2: Высота трапеции, диагонали которой взаимно перпендикулярны, равна 4. Найти площадь трапеции, если известно, что длина одной из диагоналей равна 5.

Решение: Пусть BK и CL – высоты, а O – точка пересечения диагоналей трапеции ABCD (BC – меньшее основание, BD = 5). По теореме Пифагора KD = 3. Рассмотрев треугольники AOD и ACL, замечаем, что  ∠ ACL =  ∠ BDA. Следовательно, прямоугольные треугольники BKD и ALC подобны. Отсюда BD:AC = KD:LC и, следовательно, .

.

Задача 3: Найти все натуральные числа A, оканчивающиеся цифрой 4, такие, что сумма квадратов цифр числа A не меньше A.

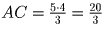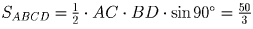Решение: Запишем искомое число A в виде (n – количество цифр в числе). Для него верна следующая оценка:

Отсюда следует, что 81(n – 1) + 12 ≥ 10^n – 1. Неравенство выполняется только при n = 1,2,3, то есть в искомом числе не более трёх цифр. Без труда находим однозначные и двузначные числа A: 4, 14, 94. Чтобы показать, что трехзначных нет, улучшим первоначальную оценку:

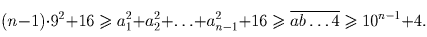
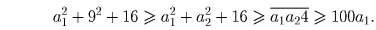
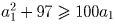Неравенство выполнено только при a₁ = 1. Осталось убедиться, что среди чисел вида 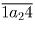нет удовлетворяющих условию.

Таким образом искомые числа 4, 14, 94.

Задача 4: Найдите все простые p, такие что 2p⁴ – p² + 16 - полный квадрат.

Решение: Если p = 3, то 2p⁴ – p² + 16 = 13². В остальных случаях p² дает остаток 1 при делении на 3 и, значит, 2p⁴ – p² + 16 дает остаток 2 при делении на 3, а квадраты такого остатка давать не могут. Таким образом, единственный ответ p = 3.