Задача 1:
Функция f такова, что для любого натурального n
1 + f(0) + f(1) + f(2) + … + f(n – 1) = f(n), f(0) = 1.
Найдите f²(0) + f²(1) + … + f²(n).
Решение:
Заметим, что f(n) = 2f(n – 1) и, значит, f(n) = 2
n. Тогда
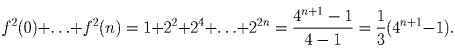
Задача 2:
Задача 3:
Задача 4:
К параболам y = – x² + 2x и y = x² + 2,5 проведены общие касательные.
Доказать, что точки касания являются вершинами параллелограмма.
Решение:
Старшие коэффициенты квадратных трёхчленов
– x² + 2x и x² + 2,5 противоположны, значит соответствующие
параболы отличаются только координатами вершин и направлением ветвей.
Рассмотрим центральную симметрию относительно точки
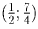
– середины отрезка между вершинами парабол:
вершины парабол перейдут друг в друга, направление ветвей изменится на
противоположное, то есть параболы перейдут друг в друга. Значит общие
касательные к параболам перейдут в общие касательные. Отсюда следует,
что четырёхугольник с вершинами в точках касания переходит сам в
себя при центральной симметрии, и, следовательно является
параллелограммом.


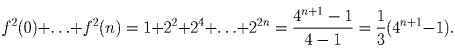
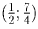 – середины отрезка между вершинами парабол:
вершины парабол перейдут друг в друга, направление ветвей изменится на
противоположное, то есть параболы перейдут друг в друга. Значит общие
касательные к параболам перейдут в общие касательные. Отсюда следует,
что четырёхугольник с вершинами в точках касания переходит сам в
себя при центральной симметрии, и, следовательно является
параллелограммом.
– середины отрезка между вершинами парабол:
вершины парабол перейдут друг в друга, направление ветвей изменится на
противоположное, то есть параболы перейдут друг в друга. Значит общие
касательные к параболам перейдут в общие касательные. Отсюда следует,
что четырёхугольник с вершинами в точках касания переходит сам в
себя при центральной симметрии, и, следовательно является
параллелограммом.