 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1980 >> Районный тур >> 9 класс ФМШ | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1980. Районный тур. 9 класс ФМШ |
|
|
Задача 2:
Задача 3:
Задача 4: p и q – простые числа. Найдите их, если известно, что уравнение x4 – px³ + q = 0 имеет целый корень.
Решение: Целый корень является делителем свободного члена уравнения, значит, может быть равен лишь ± 1 или ± q. Подставляя эти числа в уравнение, получаем
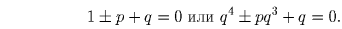
 , что невозможно; первое выполнено
лишь при p и q разной четности. Отсюда получаем единственный
ответ: p = 3,q = 2.
, что невозможно; первое выполнено
лишь при p и q разной четности. Отсюда получаем единственный
ответ: p = 3,q = 2.Задача 5: Из точки A вне окружности радиуса R проведены к ней две касательные AB и AC, где B и C – точки касания. Пусть длина отрезка BC равна a. Доказать, что
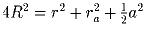 ,
где r –
радиус вписанной в треугольник ABC окружности, ra – радиус
вневписанной окружности.
,
где r –
радиус вписанной в треугольник ABC окружности, ra – радиус
вневписанной окружности.Решение: Пусть O – центр окружности, K и M – точки ее пересечения с AO. Тогда K и M – середины дуг BC. Значит, CK и CM – биссектрисы внутреннего и внешнего углов при вершине C треугольника ABC, а K и M – центры вписанной и вневписанной окружностей ∆ ABC. Отсюда r + ra = KM = 2R. Теперь достаточно проверить, что ¼a² = rra, что следует из теоремы о равенстве произведений отрезков пересекающихся хорд, примененной к хордам KM и BC.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1980 >> Районный тур >> 9 класс ФМШ | Убрать решения |