 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1981 >> Районный тур >> 10 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1981. Районный тур. 10 класс |
|
|
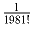 .
.Решение: Пусть положительный корень уравнения
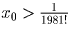 . Тогда
. Тогда
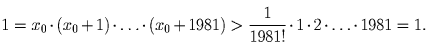
Задача 3: Найти все такие простые числа a и b, что ab + ba – тоже простое.
Решение: a и b должны быть разной четности, значит, одно из них двойка, а другое нечетное. Пусть a = 2. Тогда получаем, что 2b + b² – простое число, но при нечетном b, не делящемся на 3, 2b + b² делится на 3 и простым не является. Поэтому возможно два варианта: a = 2 и b = 3 или b = 2, a = 3.
Задача 4: Назовем сечение, проведенное в четырехугольной призме через средние линии противоположных оснований параллельно боковым ребрам, серединным сечением. Доказать, что для того, чтобы диагональные сечения, проведенные через боковые ребра, были взаимно перпендикулярны, необходимо и достаточно, чтобы серединные сечения были равновелики.
Решение: Диагональные сечения перпендикулярны тогда и только тогда, когда перпендикулярны диагонали основания. Это эквивалентно равенству средних линий основания (см. задачу 12). В этом случае серединные сечения являются параллелограммами, у которых одна и та же высота (высота призмы), и равны основания. Значит эти параллелограммы равновелики.
Задача 5: Пусть 0 < x < π /6. Доказать, что при всех натуральных n sin x + + tg ²x + sin ³x + tg 4x + … + sin 2n – 1x + tg 2nx < 1,4.
Решение: На промежутке (0; π /6) функции sin x и tg x возрастают, следовательно, оцениваемая сумма меньше, чем её значение в точке x = π /6. Значит, достаточно доказать,что
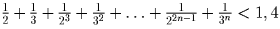 . Левая часть этого
выражения записывается в виде
. Левая часть этого
выражения записывается в виде

3x 3y 3xy 3 yx 3yx
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1981 >> Районный тур >> 10 класс | Убрать решения |