Задача 1:
Пассажир, едущий в скором поезде со скоростью 60 км/ч, видит
через окно своего вагона встречный пассажирский поезд, скорость
которого 40 км/ч. Какова длина пассажирского поезда, если пассажир
видит встречный поезд в течение 6 секунд?
Решение:
Пассажирский поезд проезжает мимо пассажира за 6 секунд, имея
относительно него скорость 100 км/ч или
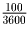
км/с.
Значит, его длина
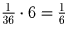
км.
Задача 2:
Можно ли натуральные числа от 1 до 21 разбить на несколько
групп, в каждой из которых наибольшее число равно сумме
остальных?
Решение:
Нельзя. Предположим, что требуемое разбиение возможно.
Тогда сумма наибольших чисел групп равняется
сумме остальных чисел, а значит сумма всех чисел от 1
до 21 четна, что не верно.
Задача 3:
a,b,c – три различные цифры. Если сложить все шесть
двузначных чисел, которые можно записать с их помощью, не
повторяя одну и ту же цифру дважды в одном числе, то получится
528. Найдите эти цифры.
Решение:
В этих числах каждая из цифр a,b,c стоит ровно по два раза
на первом и на втором местах. Значит сумма чисел равна
2 • (10 • (a + b + c) + (a + b + c)) = 528, откуда a + b + c = 24. А поскольку a,b,c – различные цифры, то возможен единственный вариант: 7, 8, 9.
Задача 4:
Квадрат 4 × 4 разграфлен прямыми, параллельными его
сторонам, на 16 одинаковых клеток. Найти 6 способов разрезания
квадрата на одинаковые части так, чтобы линия разреза шла по
сторонам клеток (способы считаются различными, если части,
получающиеся при одном способе, не равны частям, получающимся
при другом способе).
Решение: 


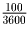 км/с.
Значит, его длина
км/с.
Значит, его длина 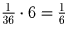 км.
Задача 2:
Можно ли натуральные числа от 1 до 21 разбить на несколько
групп, в каждой из которых наибольшее число равно сумме
остальных?
км.
Задача 2:
Можно ли натуральные числа от 1 до 21 разбить на несколько
групп, в каждой из которых наибольшее число равно сумме
остальных?