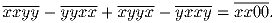Задача 1:

Задача 2: Дан угол, величина которого 82  . Пользуясь только циркулем и линейкой, построить угол в 33  .

Решение: Построим угол 60, затем угол равный 22   = 82   – 60  . Теперь построим угол 11  , разделив 22   пополам. И, наконец, – угол 33  , утроив имеющийся угол 11  .

Задача 3: Цифры x и y таковы, что выполнено равенство:

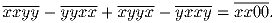
Найдите x и y.

Решение: Перепишем равенство в виде 1100x + 11y – 1100y – 11x + 1001x + 110y – 1001y – 110x = 1100x. Приведя подобные слагаемые, получаем 4x = 9y, а так как x и y – цифры, то x = 9, y = 4.

Задача 4: В треугольнике ABC проведена высота AD на основание BC. Известно, что AC > AB. Доказать, что DC – DA > AC – AB.

Решение: Если угол B тупой, то разность длин отрезков DC и BD равна длине отрезка CB и требуемое неравенство является неравенством треугольника. Если же угол B острый, то рассмотрим точку B₁, симметричную точке B относительно D, и воспользуемся доказанным неравенством для тупоугольного треугольника CAB₁.