 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1981 >> Районный тур >> 7 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1981. Районный тур. 7 класс |
|
|
Решение: По неравенству о средних 1980 • 1982 < 1981². Значит, 19801982 • 19821980 < 19812 • 1980 • 1980² < 19812 • 1981.
Задача 2: В карьере заготовленно 200 гранитных плит, 120 из которых весят по 7 тонн каждая, а остальные по 9 тонн. На железнодорожную платформу можно грузить до 40 тонн. Какое наименьшее число платформ понадобится для вывоза плит?
Решение: Понадобится 40 платформ. Общая масса плит 1560 т, следовательно, понадобится не менее 39 платформ. Но так как нагрузить платформу полностью не удаётся, то понадобится не менее 40 платформ. Такого количества действительно хватит: нужно класть на каждую платформу 2 плиты по 9 т и 3 плиты по 7 т.
Задача 3: Решить систему уравнений, если известно, что y и z – простые числа:
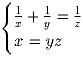
Решение: Перепишем первое уравнение в виде z(x + y) = xy. Подставив в него x из второго уравнения, получим y = z + 1. Значит y = 3, z = 2, x = 6.
Задача 4: Доказать, что для того, чтобы диагонали четырехугольника были взаимно перпендикулярны, необходимо и достаточно, чтобы средние линии четырехугольника были равны. (Средней линией четырехугольника называется отрезок, соединяющий середины противоположных сторон)
Решение: Пусть ABCD – исходный четырехугольник, KL и MN – его средние линии. Заметим, что KMLN – всегда параллелограмм, его стороны параллельны диагоналям AC и BD исходного четырехугольника, а KL и MN являются его диагоналями. Таким образом, перпендикулярность AC и BD эквивалентна тому, что KMLN – прямоугольник что, в свою очередь, равносильно тому, что у параллелограмма KMLN равны диагонали, то есть KL = MN.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1981 >> Районный тур >> 7 класс | Убрать решения |