 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 5 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1982. Районный тур. 5 класс |
|
|
Решение: Всего было 105 тонн овощей. Пусть x и y – количества овощей на складах. Тогда
 и
и
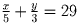 . Сложив эти два равенства, получим,
что
. Сложив эти два равенства, получим,
что 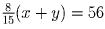 , откуда находим: x + y = 105.
, откуда находим: x + y = 105.Задача 2: В 100-этажном доме установлен лифт с двумя кнопками. Если нажать на первую кнопку, мы поднимемся на 7 этажей вверх, если нажать на вторую – спустимся на 9 этажей вниз. Как попасть с 1-го этажа на 72-й?
Решение: 4 раза « + 7», 3 раза « – 9» – попали на второй этаж. Теперь 10 раз « + 7» – попали, куда хотели.
Задача 3: В девяти клетках квадрата 3 × 3 записаны девять различных натуральных чисел, сумма которых равна 90 так, что образовался «магический квадрат", то есть сумма чисел в каждой строке, в каждом столбце и на диагоналях одна и та же. Какое число записано в центральной клетке?
Решение: Сумма всех чисел равна 90, значит сумма чисел в одной тройке (строке, столбце, диагонали) равна 30. Сложим числа в тройках, содержащих центральную клетку, а затем сложим эти четыре суммы. Получили 4 • 30, что равно сумме всех чисел, увеличенной на утроенное число из центральной клетки. Значит, в центральной клетке стоит число
 .
Задача 4:
Расставьте в каждом из чисел, где потребуется, знаки
арифметических действий и скобки между цифрами так, чтобы
результат в каждом случае равнялся 100:
.
Задача 4:
Расставьте в каждом из чисел, где потребуется, знаки
арифметических действий и скобки между цифрами так, чтобы
результат в каждом случае равнялся 100:Решение:
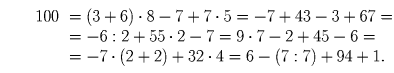
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 5 класс | Убрать решения |