 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 6 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1982. Районный тур. 6 класс |
|
|
a) В 100-этажном доме установлен лифт с двумя кнопками. Если нажать на первую кнопку, мы поднимемся на 7 этажей вверх, если нажать на вторую – спустимся на 9 этажей вниз. Как попасть с 1-го этажа на 72-й?
b) Докажите, что нельзя попасть с 4-го этажа на 5-й двадцатиэтажного дома, если нажатие на одну кнопку поднимает нас на 13 этажей, а нажатие на другую – опускает на 8 этажей.
Решение: b) На каком бы мы этаже ни находились, всегда можно нажать лишь одну кнопку лифта (или ни одной). Значит, мы можем перемещаться по этажам лишь следующим образом: 4 → 17 → 9 → 1 → 14 → 6 → 19 → 11 → 3 → 16 → 8, после чего пользоваться лифтом нельзя и, значит, нельзя с его помощью попасть на пятый этаж.
Задача 2: Найдите все 4-х значные числа вида
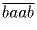 ,
которые кратны соответствующим двузначным числам
,
которые кратны соответствующим двузначным числам 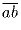 .
.Решение: Достаточно найти числа вида
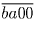 ,
кратные
,
кратные 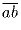 . Заметим, что
если
. Заметим, что
если 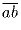 и
и 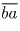 различны (то есть a ≠ b),
то они не могут иметь общих простых множителей, отличных от 2 и
3. Из условия
различны (то есть a ≠ b),
то они не могут иметь общих простых множителей, отличных от 2 и
3. Из условия 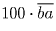 делится на
делится на 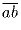 следует, что
следует, что 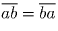 или
или 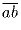 в
разложении на простые множители содержит только числа 2, 3, 5. Исходя
из этого получаем, что нам подходят следующие числа
в
разложении на простые множители содержит только числа 2, 3, 5. Исходя
из этого получаем, что нам подходят следующие числа 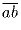 :
11; 12; 15; 18; 22; 24; 25; 33; 36; 44; 45; 48; 55; 66; 75; 77; 88;
99. Теперь нетрудно найти все искомые четырёхзначные числа.
:
11; 12; 15; 18; 22; 24; 25; 33; 36; 44; 45; 48; 55; 66; 75; 77; 88;
99. Теперь нетрудно найти все искомые четырёхзначные числа.Задача 3:
Задача 4: На стороне OA угла AOB отложены отрезки OC и OK (OK > OC), а на стороне OB – соответственно равные им отрезки OD и OM. Пусть H – точка пересечения прямых CM и DK. Докажите, что точка H лежит на биссектрисе угла AOB.
Решение: Отразим картинку симметрично относительно биссектрисы угла O. При этом точки C и D, а так же K и M перейдут друг в друга. Значит перейдут друг в друга отрезки CM и DK . Следовательно, точка их пересечения, остающаяся неподвижной, лежит на биссектрисе угла O.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 6 класс | Убрать решения |