Задача 1:
Задача 2:
Какое наибольшее количество чисел можно выбрать среди
натуральных чисел от 1 до 100 так, чтобы сумма любых двух
выбранных делилась на 6?
Решение:
Так как сумма любых двух чисел делится на 6, то остатки всех
чисел при делении на шесть одинаковы и, следовательно, равны 0
или 3. Чисел, дающих остаток 3, среди чисел от 1 до 100
семнадцать, а кратных 6 – всего 16. Значит, можно выбрать 17
чисел: 3,9, … ,99.
Задача 3:
В треугольнике ABC, в котором ∠ A < ∠ B < ∠ C,
проведены биссектрисы внешних углов при вершинах A и C до
пересечения с продолжениями противоположных сторон в точках D и
E. Оказалось, что AD = CE = AC. Найти величины углов треугольника
ABC.
Решение:
Биссектриса внешнего угла треугольника пересекает продолжение
противоположной стороны так, что вершина, соответствующая
большему из противолежащих углов, оказывается между вершиной,
соответствующей меньшему из них, и точкой пересечения.
Обозначим углы треугольника ABC через α , β , γ .
Тогда
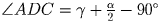
,
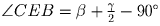
. Воспользуемся тем,
что треугольники ADC и ACE равнобедренные:
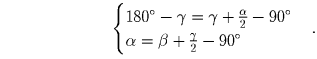
Решив эту систему,
найдем углы треугольника ABC: α = 12
, β = 36
, γ = 132
.
Задача 4:
a,b,c – натуральные числа. Докажите, что значение выражения
a³(b – c) + b³(c – a) + c³(a – b)
кратно сумме a + b + c.
Решение:
Перепишем выражение в виде ab(a² – b²) + ac(c² – a²) + bc(b² – c²).
Заметим, что заменив (a + b) на ( – c),(b + c) на ( – a),(a + c) на
( – b), мы не изменим остатков от деления на (a + b + c), так как эти
выражения при делении на (a + b + c) дают одинаковые остатки. После
такой замены исходное выражение примет вид

.


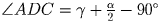 ,
, 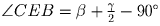 . Воспользуемся тем,
что треугольники ADC и ACE равнобедренные:
. Воспользуемся тем,
что треугольники ADC и ACE равнобедренные: 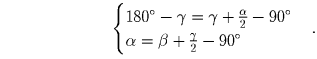
 .
.