 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 8 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1982. Районный тур. 8 класс |
|
|
Решение: Пусть искомое число равно 2k + 1 или 2k + 2. Тогда сумма предшествующих чётных чисел 2 + 4 + … + 2k равна k(k + 1). Составим уравнения:
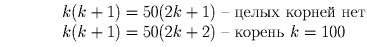
Решение: Нельзя. Наибольшая сумма, которую можно получить из этих цифр равна + 5, наименьшая равна – 5. Всего различных сумм 11, а нужно 12 (пять строк, пять столбцов, две диагонали).
Задача 3: Диагонали трапеции взаимно перпендикулярны. Докажите, что произведение длин оснований трапеции равно сумме произведений длин отрезков одной диагонали и длин отрезков другой диагонали, на которое они разбиваются точкой пересечения.
Решение: Пусть O – точка пересечения диагоналей трапеции ABCD (AB и CD – основания). Воспользуемся подобием треугольников ABO и CDO:
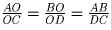 .
Отсюда получаем, что
.
Отсюда получаем, что 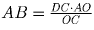 ;
; 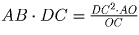 . Подставив DO² + OC² вместо
DC², получим
. Подставив DO² + OC² вместо
DC², получим
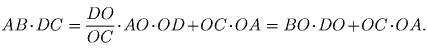
Задача 5: O – произвольная точка медианы AA1 треугольника ABC. Прямая BO пересекает сторону AC в точке B1. Прямая CO пересекает сторону AB в точке C1. Докажите, что B1C1 параллельно BC.
Решение: Из условий
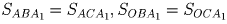 заключаем, что SABO = SACO.
Заметим, что
заключаем, что SABO = SACO.
Заметим, что
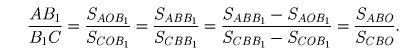
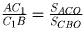 . Воспользовавшись
равенством площадей треугольников ABO и ACO, получаем, что
. Воспользовавшись
равенством площадей треугольников ABO и ACO, получаем, что
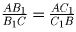 , то есть прямые B1C1
и BC параллельны.
, то есть прямые B1C1
и BC параллельны.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 8 класс | Убрать решения |