 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 9 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1982. Районный тур. 9 класс |
|
|
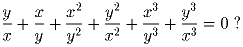
Решение: Если x и y одного знака, то левая часть положительна. Если x и y разного знака, то все слагаемые, кроме квадратов отрицательны. Одно из слагаемых
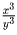 и
и 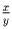 по модулю не меньше, чем
по модулю не меньше, чем 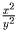 и, значит,
сумма
и, значит,
сумма 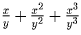 отрицательна. Проделав те же рассуждения для трех оставшихся
слагаемых, получим, что вся сумма отрицательна. Таким образом,
уравнение вещественных корней не имеет.
отрицательна. Проделав те же рассуждения для трех оставшихся
слагаемых, получим, что вся сумма отрицательна. Таким образом,
уравнение вещественных корней не имеет.Задача 2: Доказать, что касательные, проведенные к параболе y = ½x² из точки
 , взаимно перпендикулярны.
, взаимно перпендикулярны.Решение: Касательная к параболе y = ½x² в точке (x0;y0) имеет уравнение
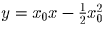 .
Эта касательная проходит через точку
.
Эта касательная проходит через точку
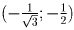 при
при
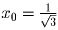 или
или 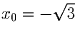 . Получили, что
касательные, проведенные из точки
. Получили, что
касательные, проведенные из точки 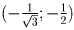 имеют угловые коэффициенты
имеют угловые коэффициенты 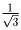 и
и 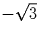 ,
что и означает их перпендикулярность.
Задача 3:
В конечной возрастающей арифметической прогрессии сумма двух
каких-то последовательных членов, среди которых нет первого,
равна члену, следующему за ними. Найти прогрессию, если сумма её
членов равна 11d (d – разность прогрессии).
,
что и означает их перпендикулярность.
Задача 3:
В конечной возрастающей арифметической прогрессии сумма двух
каких-то последовательных членов, среди которых нет первого,
равна члену, следующему за ними. Найти прогрессию, если сумма её
членов равна 11d (d – разность прогрессии).Решение: ak + ak + 1 = ak + 2, откуда ak = d (d – разность прогрессии). Значит прогрессия имеет вид: … , – d,0,d,2d,3d, … . Пусть md и nd – первый и последний члены прогрессии. Так как ak – не первый член прогрессии, то m < 0. Вычислим сумму прогрессии:
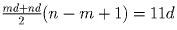 ,
откуда (m + n)(n – m + 1) = 22. Поскольку оба сомножителя целые и
n – m + 1 > 0, то получаем два варианта:
,
откуда (m + n)(n – m + 1) = 22. Поскольку оба сомножителя целые и
n – m + 1 > 0, то получаем два варианта: 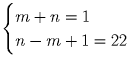 или
или 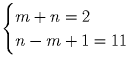 . Решив эти
системы, заключаем, что прогрессия имеет вид – 4d, – 3d, … ,6d или – 10d, – 9d, … ,11d.
. Решив эти
системы, заключаем, что прогрессия имеет вид – 4d, – 3d, … ,6d или – 10d, – 9d, … ,11d.Задача 4: ABCD – вписанный в окружность четырехугольник, причем известно, что диагональ AC – биссектриса угла DAB. Докажите, что AC • BD = AD • DC + AB • BC.
Решение:
Из свойств вписанных углов, заключаем, что
∠ CBD = ∠ CAD = ∠ CAB = ∠ CDB
и, следовательно, треугольники ABC и BOC, а также ADC и DOC,
подобны (O – точка пересечения диагоналей). Значит, 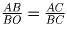 и
и 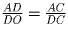 , откуда
AB • BC + AD • DC = AC • BO + AC • DO = AC • DB.
, откуда
AB • BC + AD • DC = AC • BO + AC • DO = AC • DB.
Задача 5: Найдите все такие натуральные числа x,y,z, что равенство xn + yn = zn + 1 имеет место при любом натуральном n.
Решение: Запишем данное равенство при n = 1 и n = 2 и выразим произведение xy:
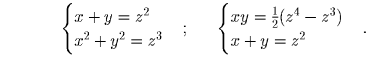
Из условия неотрицательности дискриминанта: 2z³ – z4 ≥ 0 находим, что z может принимать только значения 1 и 2. Натуральные корни уравнение имеет только при z = 2. Ответ: x = y = z = 2.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1982 >> Районный тур >> 9 класс | Убрать решения |