Задача 1:

Задача 2: Найти такое наименьшее натуральное число k, что композиция k поворотов на 19   является поворотом на 10  .

Решение: Нужно найти минимальное натуральное k, при котором 19k = 360n ± 10. Запишем равенство в виде 19k – 361n =  + 10 – n. Его левая часть должна делиться на 19. Минимальное натуральное n, при котором это возможно, равно 9. Значит, наш ответ: k = 19n – 1 = 170.

Задача 3:

Задача 4: ABCD – вписанный в окружность четырехугольник. A₁,B₁,C₁,D₁ – середины дуг AB, AC, CD, DA соответственно. Докажите, что

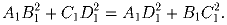
Задача 5: Найдите все такие натуральные числа x, y, z, что равенство 989xⁿ + 993yⁿ = z^n + 1 верно при всех натуральных n.

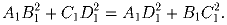
Решение: Решая аналогично задаче 82.22, получаем квадратное уравнение с дискриминантом , который должен быть точным квадратом. Для этого необходимо, чтобы z • (993 + 989 – z) делилось на 993 • 989, что возможно лишь при трёх натуральных значениях z: z = 993, z = 989, z = 989 + 993 = 1982. Отсюда получаем единственное решение: x = y = z = 1982.