Задача 1:
Углы треугольника образуют арифметическую прогрессию, синусы
удвадцатеренных углов, взятых в той же последовательности, также
образуют арифметическую прогрессию. Найдите углы треугольника.
Решение:
Пусть α , β , γ – углы треугольника,
α ≤ β ≤ γ . Тогда α + γ = 2 β и,
следовательно, β = 60
, α = 60
– x, γ = 60
+ x. Известно, что sin 20 α + sin 20 γ = 2 sin 20 β , тогда по формуле суммы синусов 2 sin 10( α + γ ) • cos 10( α – γ ) = 2 sin 20 β . Отсюда
cos 10( α – γ ) = 1, 10( α – γ ) = 2 π n, то есть
20x = 2 π n (n – целое число);

. Помня
о том, что 0
≤ x ≤ 60
, получаем возможные
варианты: x = 0,
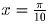
,
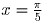
,
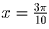
. Значит, треугольник может иметь углы:
(60°,60°,60°);
(42°,60°,78°);
(24°,60°,96°);
(6°,60°,114°).
Задача 2:
Найдите какую-нибудь первообразную функции f(x) = ctg ²x.
Решение:
Записав
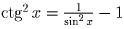
, видим, что функция
f(x) = – ctg x – x является требуемой первообразной.
Задача 3:
Задача 4:
К параболе y = x² – 0,25 проведены две касательные так, что точки
касания и точка пересечения касательных являются вершинами
равностороннего треугольника. Докажите, что начало координат
является центром этого треугольника.
Решение:
Касательные к параболе
в точках (x
1;y
1), (x
2;y
2) имеют уравнения

и
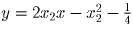
, абсцисса их точки пересечения
равна
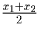
.
Для того, чтобы
эта точка была равноудалена от точек касания необходимо, чтобы
выполнялось равенство y
1 = y
2 и, следовательно,
x
1 = – x
2. Получили, что картинка симметрична относительно
оси Oy, то есть касательные имеют углы наклона
60
и 120
. Тогда
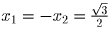
и наш равносторонний
треугольник имеет вершины в точках
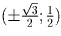
и (0; – 1). Одна из его медиан лежит на оси Oy и делится
началом координат в отношении 1:½, то есть 2:1.
Значит, начало координат является центром этого треугольника.
Задача 5:


 . Помня
о том, что 0 ≤ x ≤ 60 , получаем возможные
варианты: x = 0,
. Помня
о том, что 0 ≤ x ≤ 60 , получаем возможные
варианты: x = 0, 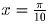 ,
, 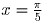 ,
,
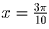 . Значит, треугольник может иметь углы:
(60°,60°,60°);
(42°,60°,78°);
(24°,60°,96°);
(6°,60°,114°).
Задача 2:
Найдите какую-нибудь первообразную функции f(x) = ctg ²x.
. Значит, треугольник может иметь углы:
(60°,60°,60°);
(42°,60°,78°);
(24°,60°,96°);
(6°,60°,114°).
Задача 2:
Найдите какую-нибудь первообразную функции f(x) = ctg ²x.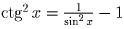 , видим, что функция
f(x) = – ctg x – x является требуемой первообразной.
, видим, что функция
f(x) = – ctg x – x является требуемой первообразной. и
и
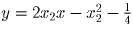 , абсцисса их точки пересечения
равна
, абсцисса их точки пересечения
равна 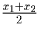 .
Для того, чтобы
эта точка была равноудалена от точек касания необходимо, чтобы
выполнялось равенство y1 = y2 и, следовательно,
x1 = – x2. Получили, что картинка симметрична относительно
оси Oy, то есть касательные имеют углы наклона
60 и 120 . Тогда
.
Для того, чтобы
эта точка была равноудалена от точек касания необходимо, чтобы
выполнялось равенство y1 = y2 и, следовательно,
x1 = – x2. Получили, что картинка симметрична относительно
оси Oy, то есть касательные имеют углы наклона
60 и 120 . Тогда
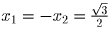 и наш равносторонний
треугольник имеет вершины в точках
и наш равносторонний
треугольник имеет вершины в точках 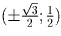 и (0; – 1). Одна из его медиан лежит на оси Oy и делится
началом координат в отношении 1:½, то есть 2:1.
Значит, начало координат является центром этого треугольника.
и (0; – 1). Одна из его медиан лежит на оси Oy и делится
началом координат в отношении 1:½, то есть 2:1.
Значит, начало координат является центром этого треугольника.