 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1983 >> Районный тур >> 5 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1983. Районный тур. 5 класс |
|
|
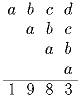
Решение: a = 1, значит b = 8 или b = 7. Если b = 8, то c + 8 + 1 ≤ 8, чего быть не может. Следовательно, b = 7. Отсюда получаем, что c = 8,d = 7. Задача 2: Докажите, что при перемножении трех тысяч двоек получается число не более, чем из 1000 цифр.
Решение: 2³ººº = 8¹ººº < 10¹ººº, а это наименьшее число из 1001 цифры. Значит, в числе 2³ººº цифр не более 1000.
Задача 3: Разрежьте квадрат на два равных девятиугольника. Покажите ответ на рисунке.
Решение:
Например, так 2exto 1truecmem:graph katris1.pcx !!!!!!!!!!!!!КАРТИНКА!!!!!!!!!!!!
Задача 4: Два пешехода стартовали одновременно по круговой дороге с одного места в одном направлении. Пешеход, идущий быстрее, нагнал другого через 36 минут. Если бы они стартовали в противоположных направлениях, то встретились бы через 4 минуты. За сколько минут каждый из пешеходов может обойти круговую дорогу?
Решение: Пусть их скорости v1 и v2, l – длина круговой дороги. Из условий получаем:
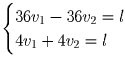 ,
откуда
,
откуда 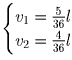 .
Время, которое потратят пешеходы на всю дорогу:
.
Время, которое потратят пешеходы на всю дорогу: 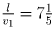 мин.,
мин., 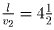 мин.
мин.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1983 >> Районный тур >> 5 класс | Убрать решения |