Задача 1: Какие две цифры нужно приписать справа к числу 1983, чтобы получилось число, делящееся на 83?

Решение: Запишем условие в виде 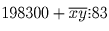. Первое слагаемое при делении на 83 дает остаток 13. Значит, 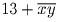делится на 83, из чего заключаем, что 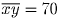, то есть нужно приписать цифры 7 и 0.

Задача 2: В произвольном 4-хзначном числе вычеркнули поочередно каждую из цифр и сложили образовавшиеся 4 числа. Докажите, что полученная сумма делится на 9 в том и только том случае, когда исходное число делится на 3.

Решение: Пусть исходное число .

Значит всё выражение делится на 9 тогда и только тогда, когда a + b + c + d делится на 3, а это условие равносильно тому, что на 3 делится исходное число .

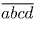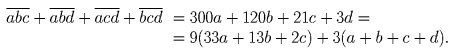
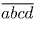Задача 3: В 6^A классе провели контрольную работе по алгебре. Средняя оценка у мальчиков оказалась 4, у девочек 3,25, а у всех вместе 3,6. Сколько мальчиков и сколько девочек решали контрольную работу, если в класса больше 30-ти, но меньше 50-ти человек.

Решение: Пусть в классе x мальчиков и y девочек. Тогда сумма всех оценок, полученных мальчиками, равна 4x, девочками – 3,25y, средний балл равен 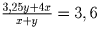. Отсюда получаем, что 7y = 8x. Следовательно, y = 8k, а x = 7k при некотором натуральном k. Тогда x + y = 15k, а число такого вида в интервале от 30 до 50 только одно: x + y = 45. Значит, в классе 24 девочки и 21 мальчик.

Задача 4: Докажите, что если основание, угол при основании и сумма боковых сторон одного треугольника соответственно равны основанию, углу при основании и сумме боковых сторон другого треугольника, то эти треугольники равны.

Решение:

Пусть AC = A₁C₁,  ∠ A =  ∠ A₁, AB + BC = A₁B₁ + B₁C₁. Продолжив стороны AB и A₁B₁, отложим на них отрезки BD и B₁D₁ соответственно так, чтобы BD = BC, B₁D₁ = B₁C₁. Тогда AD = A₁D₁ и, следовательно,  ∆ ADC =  ∆ A₁D₁C₁ по первому признаку. Отсюда следует, что  ∠ D =  ∠ D₁,  ∠ ACD =  ∠ A₁C₁D₁, а так как  ∆ CBD и  ∆ C₁B₁D₁ равнобедренные, то  ∠ ACB =  ∠ A₁C₁B₁. Теперь к треугольникам ABC и A₁B₁C₁ применим второй признак равенства треугольников.