Задача 1: В равнобедренном треугольнике ABC с вершиной A и основанием BC проведена биссектриса CC₁. Найти углы треугольника, если CC₁ = AC₁.

Решение: Пусть  ∠ A =  α . Тогда  ∠ ACC₁ =  α , так как  ∆ ACC₁ равнобедренный.  ∠ ACB =  ∠ ABC = 2 α ; сумма углов треугольника ABC равна 5 α . Следовательно,  α  = 36  . Таким образом, углы треугольника ABC: 36  ,72  ,72  .

Задача 2:

Задача 3: Докажите, что число 1004041 составное.

Решение: 1004041 = (10⁶ + 1) + 4 • 10 • (10² + 1). Воспользовавшись формулой суммы кубов, получим разложение на множители: (10² + 1) • ((10⁴ – 10² + 1) + 4 • 10).

Задача 4: Известно, что

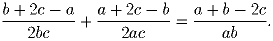
Найти значение выражения: .

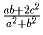
Решение: Данное в условии равенство преобразуется к виду (a – b)² = 4c². Тогда a² + b² = 4c² + 2ab и, следовательно, .
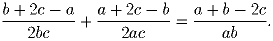
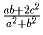