Задача 1:
Задача 2:
Найдите два трехзначных числа, если известно, что сумма
остальных трехзначных чисел в 600 раз больше одного из этих
чисел.
Решение:
Сумма всех трехзначных чисел равна
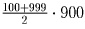
. Пусть
искомые числа x и y, тогда

; 494550 = 601x + y. Так как 100 ≤ y ≤ 999, то
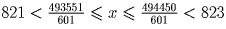
.
Значит, x = 822,y = 528.
Задача 3:
Задача 4:
Решите в целых числах уравнение: x² – 4xy + 3y² = 1983.
Решение:
Разложим обе части равенства на множители: (x – y)(x – 3y) = 3 • 661. Сомножители в левой части могут быть лишь числам ± 1;
± 3; ± 661; ± 1983. Решив получившиеся восемь систем,
получим восемь возможных пар (x;y):
( + 990; ± 991),( + 2974; ± 991),( + 326; ± 329),( + 990; ± 329)
(знаки надо выбирать одинаковые).
Задача 5:
Сечение параллелепипеда плоскостью – пятиугольник с четырьмя
равными углами. Найдите углы этого пятиугольника.
Решение:
Плоскость пересекает пять из шести граней параллелепипеда.
Значит, получившийся в сечении пятиугольник ABCDE будет иметь
две пары параллельных сторон. Пусть AB || DE и
AE || CD. Продолжим AB
и CD до пересечения в точке K. AKDE – параллелограмм. Если
∠ D = ∠ E, то эти углы прямые. Тогда в
ABCDE получается 4 прямых угла, что невозможно. Значит ∠ D ≠ ∠ E, а ∠ A = ∠ ABC = ∠ BCD = ∠ D.
Тогда ∠ K = ∠ KBA = ∠ BCK, как углы дополняющие равные
до 180. Значит, ∠ K = ∠ E = 60
, то есть
один угол сечения 60
, а остальные – по 120
.


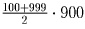 . Пусть
искомые числа x и y, тогда
. Пусть
искомые числа x и y, тогда  ; 494550 = 601x + y. Так как 100 ≤ y ≤ 999, то
; 494550 = 601x + y. Так как 100 ≤ y ≤ 999, то
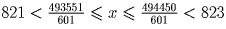 .
Значит, x = 822,y = 528.
.
Значит, x = 822,y = 528.