Задача 1:

Задача 2:

Задача 3: На одной стороне угла с вершиной O отложены равные отрезки OA = AB = BC, на другой – отрезки OD = DE = EF. Пусть M – точка пересечения AE и BD, P – точка пересечения BF и CE. Докажите, что точки O,M,P лежат на одной прямой.

Решение: Заметим, что прямые AD, BE и CF параллельны и воспользуемся тем, что в трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой. Пусть X – середина BE. Рассматривая сначала трапецию ABED, а затем трапецию BCFE, заключаем, что точки точки O, M, X лежат на одной прямой, точки O, P, X лежат на одной прямой и, следовательно, точки O, M, P лежат на одной прямой.

Задача 4: Решить уравнение: x³ + x² + x =  – ⅓.

Решение: 3x³ + 3x² + 3x + 1 = 0; (x + 1)³ =  – 2x³ ; ; .

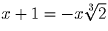
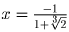
Задача 5:
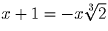
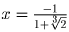