Задача 1:
Найдите наименьшее натуральное число, которое увеличивается в
целое число раз (большее 1) при переносе его последней цифры в
начало.
Решение:
Аналогично задаче 12 запишем

, 1 < k < 10, откуда
(k • 10
n – 10
n – 1)a
n + … + (k • 10 – 1)a
1 = (10
n – k)a
0 и, следовательно,
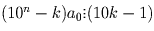
. Наименьшее n, при котором это
возможно равно 5:

при a
0 = 3;6;9;
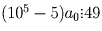
при a
0 = 7. Находим
соответствующие числа: 076923 • 4 = 307692, 153846 • 4 = 615384, 230769 • 4 = 923076, 142857 • 5 = 714285. Первый
вариант некорректен, а из остальных наименьшем является число
142857.
Задача 2:
Задача 3:
Докажите, что
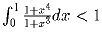
.
Решение:
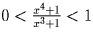
при 0 < x < 1.
Значит
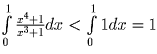
.
Задача 4:
Докажите, что уравнение x
4 + 5x³ – x² – 3x – 1 = 0 имеет не более одного
положительного корня.
Решение:
Если положительных корней два или четыре, то f(0) должно быть
положительным, что не так. Докажем, что положительных корней не
может быть три. Как известно, любой многочлен четвёртой степени можно
представить в виде произведения двух квадратных трёхчленов
с вещественными коэффициентами. Тогда
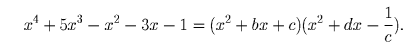
У одного из трёхчленов (пусть у
первого) оба корня положительны, то есть c > 0,b < 0. Приравнивая
коэффициэнты при соответствующих степенях x произведения
трехчленов и исходного многочлена, получаем
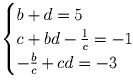
. Пользуясь тем,
что знаки b и c известны, заключаем из первого уравнения, что
d > 0, а из третьего, что d < 0. Пришли к противоречию, которое и
доказывает наше утверждение.
Задача 5:
Докажите, что если a, b – длины катетов, а c – длина
гипотенузы прямоугольного треугольника, то ab(a + b + c) < 1,25c³.
Решение:
Воспользовавшись тем, что

и

, получаем
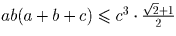
. Остаётся проверить, что

.


 , 1 < k < 10, откуда
(k • 10n – 10n – 1)an + … + (k • 10 – 1)a1 = (10n – k)a0 и, следовательно,
, 1 < k < 10, откуда
(k • 10n – 10n – 1)an + … + (k • 10 – 1)a1 = (10n – k)a0 и, следовательно, 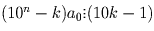 . Наименьшее n, при котором это
возможно равно 5:
. Наименьшее n, при котором это
возможно равно 5:  при a0 = 3;6;9;
при a0 = 3;6;9;
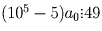 при a0 = 7. Находим
соответствующие числа: 076923 • 4 = 307692, 153846 • 4 = 615384, 230769 • 4 = 923076, 142857 • 5 = 714285. Первый
вариант некорректен, а из остальных наименьшем является число
142857.
Задача 2:
при a0 = 7. Находим
соответствующие числа: 076923 • 4 = 307692, 153846 • 4 = 615384, 230769 • 4 = 923076, 142857 • 5 = 714285. Первый
вариант некорректен, а из остальных наименьшем является число
142857.
Задача 2: 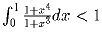 .
.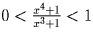 при 0 < x < 1.
Значит
при 0 < x < 1.
Значит 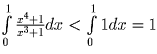 .
Задача 4:
Докажите, что уравнение x4 + 5x³ – x² – 3x – 1 = 0 имеет не более одного
положительного корня.
.
Задача 4:
Докажите, что уравнение x4 + 5x³ – x² – 3x – 1 = 0 имеет не более одного
положительного корня.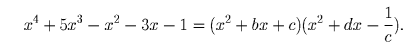
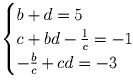 . Пользуясь тем,
что знаки b и c известны, заключаем из первого уравнения, что
d > 0, а из третьего, что d < 0. Пришли к противоречию, которое и
доказывает наше утверждение.
Задача 5:
Докажите, что если a, b – длины катетов, а c – длина
гипотенузы прямоугольного треугольника, то ab(a + b + c) < 1,25c³.
. Пользуясь тем,
что знаки b и c известны, заключаем из первого уравнения, что
d > 0, а из третьего, что d < 0. Пришли к противоречию, которое и
доказывает наше утверждение.
Задача 5:
Докажите, что если a, b – длины катетов, а c – длина
гипотенузы прямоугольного треугольника, то ab(a + b + c) < 1,25c³. и
и  , получаем
, получаем 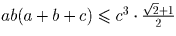 . Остаётся проверить, что
. Остаётся проверить, что
 .
.