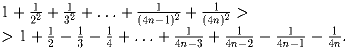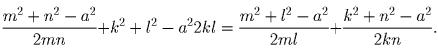Задача 1:
Задача 2:
Задача 3:
Две касательные, проведенные к параболе y = x² + x, взаимно
перпендикулярны. Докажите, что расстояние между точками касания
не меньше 1.
Решение:
Заметим, что вместо параболы y = x² + x можно рассматривать
параболу y = x². Касательная к ней в точке x
1
имеет угловой коэффициэнт 2x
1. Для того, чтобы касательные,
проведенные в точках x
1 и x
2 были перпендикулярны, необходимо и
достаточно, чтобы 2x
1 • 2x
2 = – 1, то есть
x
1x
2 = – ¼. Расстояние между точками касания не
меньше расстояния между их проекциями на ось Ox, которое равно
|x
1 – x
2|. Поскольку x
1x
2 < 0, то
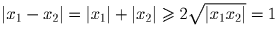
. Что и
требовалось.
Задача 4:
Доказать неравенство:
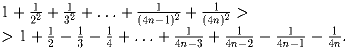
Решение:
Аналогично задаче 3 9-го класса (ФМШ).
Задача 5:
Основанием пирамиды является ромб, а суммы косинусов
противоположных плоских углов при вершинах пирамиды равны.
Докажите, что одна из диагоналей основания перпендикулярна
плоскости диагонального сечения пирамиды.
Решение:
KLMNO- пирамида. Пусть a – длина стороны основания,
k, l, m, n –
боковые ребра. Выразим косинусы плоских углов при вершине O по
теореме косинусов, применив ее к каждой из боковых граней и
запишем условие на эти косинусы в виде
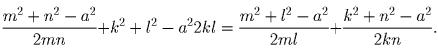
Домножая на 2klmn,
преобразуем к виду
(mk + ln)(l – n)(m – k) = a²(l – n)(k – m),
откуда l = n
или m = k. Пусть (для определенности) l = n. Тогда точка O
равноудалена от L и N и, значит, лежит в плоскости,
перпендикулярной LN, проходящей через середину LN. Это и
означает, что плоскость диагонального сечения KON
перпендикулярна диагонали LN.


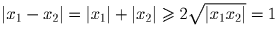 . Что и
требовалось.
Задача 4:
Доказать неравенство:
. Что и
требовалось.
Задача 4:
Доказать неравенство: