 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1984 >> Районный тур >> 7 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1984. Районный тур. 7 класс |
|
|
Решение:
 .
Возведем второе уравнение в квадрат и, использовав
первое, получим (x + y)² = (t + z)², откуда x + y = t + z или x + y = – t – z.
Рассморев сумму и разность полученного равенства и второго уравнения
системы, получим требуемое.
.
Возведем второе уравнение в квадрат и, использовав
первое, получим (x + y)² = (t + z)², откуда x + y = t + z или x + y = – t – z.
Рассморев сумму и разность полученного равенства и второго уравнения
системы, получим требуемое.Задача 2: На сторонах AB и AC треугольника ABC выбраны точки C1 и B1 так, что ∠ ABB1 = 5 , ∠ ACC1 = 10 . Найдите углы треугольника AB1C1, если ∠ ABC = 60 , ∠ ACB = 70 .
Решение: ∠ A = 50. Чтобы найти остальные углы треугольника AB1C1, заметим, что треугольник C1BC – равносторонний, треугольник B1CB – равнобедренный (B1C = BC), так как ∠ BB1C = ∠ B1BC = 55 . Значит, B1C = BC = CC1, то есть треугольник C1B1C равнобедренный. Следовательно,
 .
Отсюда находим, что ∠ AB1C1 = 180° – 85° = 95 , ∠ AC1B1 = 180° – 85° – 60° = 35 .
Задача 3:
Докажите, что a) 1,01¹ººº > 10.
b) 1,01¹ººº > 1000.
.
Отсюда находим, что ∠ AB1C1 = 180° – 85° = 95 , ∠ AC1B1 = 180° – 85° – 60° = 35 .
Задача 3:
Докажите, что a) 1,01¹ººº > 10.
b) 1,01¹ººº > 1000.Решение: a) При умножении числа на 1,01 к нему прибавляется его сотая часть. При умножении числа, большего 1, на 1,01 к нему прибавляется больше, чем 0,01. При умножении 1,01 • 1,01 • … • 1,01 (1000 раз) к числу 1,01 прибавляется больше, чем 999 • 0,01, то есть 1,01¹ººº > 1,01 + 0,01 • 999 = 11, что и требовалось.
b) 1,01¹ººº = (1,01¹ºº)¹º > (1,01 + 99 • 0,01)¹º = 2¹º = 1024 > 1000.
Задача 4: Найдите наименьшее натуральное число, которое увеличивается в пять раз при переносе его последней цифры в начало.
Решение: Пусть искомое число имеет вид
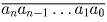 . Условие записывается в
виде
. Условие записывается в
виде 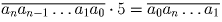 . Отсюда:
(5 • 10n – 10n – 1)an + (5 • 10n – 1 – 10n – 2)an – 1 + … + (5 • 10 – 1)a1 = (10n – 5)a0.
Каждое слагаемое в левой части
делится на 5 • 10 – 1 = 49. Значит, 10n – 5 делится на 7.
Минимальное n при котором это возможно равно 5, тогда a0 = 7.
Отсюда искомое число 142857.
. Отсюда:
(5 • 10n – 10n – 1)an + (5 • 10n – 1 – 10n – 2)an – 1 + … + (5 • 10 – 1)a1 = (10n – 5)a0.
Каждое слагаемое в левой части
делится на 5 • 10 – 1 = 49. Значит, 10n – 5 делится на 7.
Минимальное n при котором это возможно равно 5, тогда a0 = 7.
Отсюда искомое число 142857.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1984 >> Районный тур >> 7 класс | Убрать решения |