 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1984 >> Районный тур >> 8 класс | Убрать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1984. Районный тур. 8 класс |
|
|
Решение: Перепишем уравнение в виде – 1984 = x(x – 1)(x – 2). 1984 не делится на 3 и, следовательно, не может быть представлено в виде произведения трех последовательных целых чисел. Значит, целых корней уравнение не имеет. Задача 2: Точка D – середина основания BC равнобедренного треугольника ABC. На отрезке AB взяли точку M так, что AM = ⅓AB. Найдите ∠ MCB, если известно, что AD = BC.
Решение: Пусть K – середина MB, X – середина DK. Тогда DK || CM, MX || AD (как средние линии треугольников CBM и ADK соответственно), MX = ½AD. Но, так как OMXD – параллелограмм (O – точка пересечения MC и AD), то MX = OD и, следовательно, O – середина AD. Значит, треугольник ODC равнобедренный и, следовательно, ∠ MCB = 45 . Задача 3: Что больше:
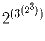 или
или 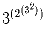 ?
?Решение: 34 > 25, 38 > 2¹º, значит
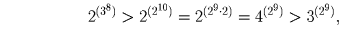
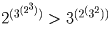 .
.Задача 4: На сторонах AB, BC и AC треугольника ABC вне него построены квадраты; AM, BN, CK – стороны этих квадратов, перпендикулярные сторонам AB, BC, AC соответственно. Докажите, что
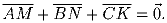
Решение: Рассмотрим вектора, полученные из
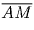 ,
, 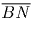 ,
,
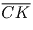 поворотом на 90 . Они равны векторам
поворотом на 90 . Они равны векторам
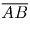 ,
,  ,
,  соответственно, сумма
которых равна
соответственно, сумма
которых равна 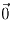 . Значит, и сумма исходных векторов равна
. Значит, и сумма исходных векторов равна
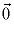 .
Задача 5:
Про вещественные числа a, b и c известно, что
.
Задача 5:
Про вещественные числа a, b и c известно, что
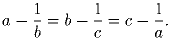
Решение: Условие можно переписать в виде трех равенств:
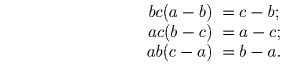
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1984 >> Районный тур >> 8 класс | Убрать решения |